教学设计

课时授课计划

章节题目		直角三角形中正切与余切				授课时间	6月15日
设计依据	《数学教学大纲》中明确指出：学生要能够解决带有实际意义的数学问题，对周围现象要具有好奇心，不断追求新知、独立思考，会从数学的角度发现和提出问题，并用数学方法加以探索、研究和解决，使数学学习成为再发现、再创造的过程。本节课的设计正是基于该理念，从一个学生目前不能解决的问题出发，引导学生去探索数学新知——直角三角形的四个三角函数值，使问题得以解决，达到培养应用数学意识，激发学习数学的热情。
学情分析	能力储备：学生聪明，勤于思考，喜欢探索，求知欲强。有合作意识，分工明确，协作能力强。知识储备：会求正方形、长方形、梯形、圆等图形的面积和周长；能够使用几何画板度量线段长度和角度，并能利用几何画板计算和差及比值。
目标教学	让学生在探索、求知中体味数学的实用性，形成良好的思维品质，提高思维水平；通过对具体问题的解决，养成认真、严谨的学风；面对认识上的危机，要敢于挑战自我，超越自我，从而形成坚强的意志品质。
教学重点	利用几何画板发现我们肉眼所不能发现的问题，突出数学的严谨性、科学性。
教学难点	对由正方形到长方形的剪拼的不可能性的认识
课型	新课		教法	任务驱动法	学法		探究与实验
教具	尺子、计算机		预测达成度	70%	实际达成度
板书设计	图形（1）图形（2）正切余切的定义性质
流程图

教学过程

阶段目标	教师活动	学生活动	设计意图
情景导入	丢失的面积哪去了如图，有一个边长为13的正方形ABCD，按图中所示的方法将它分割成两个直角三角形和两个梯形，再将这个正方形沿虚线剪开，得到四个小图形。有位同学用这四个小图形拼了一个长方形EFGH。当计算它们的面积时，却发现正方形的面积是13×13=169，而长方形的面积为8×21=168，丢失的面积哪去了？	审题、思考小组讨论——问题出在哪了	调动学生的思维热情
实验探究	1、动手做一做学生剪拼准备好的正方形； 2、利用几何画板度量角度度量∠GMQ与∠EMQ的度数，并计算两角的和。 3、利用几何画板探求正切余切	动手实验和测量	实验操作分析解决问题
理论支持	l 利用直角三角形解决问题 1、使用几何画板探究直角三角形的正切值、余切值——定值给出正切余切的定义 2、操作得出“角度相等，正切值或余切值相等” （见实验班教材《几何》第三册1页—8页） 3、启发学生学以致用，利用正切、余切解决该问题 4、口答练习（题目由学生和老师自编） l 相似三角形——简单说明见实验班教材《几何》第四册193页--205页	学生了解正切余切的内容，有一个初步认识，能简单应用	数学魅力所在
反思小结	1、学生谈一谈自己的心得 2、教师补充	学生畅谈	培养善思善结的学习习惯
当堂检测	1、如图，在Rt△ABC中，AC=2，BC=4，则tanA= ； A 2 B 4 C D 1 　 2、如图，在Rt△ABC中，AC=1.5，BC=4.5，则cotA= ； A 1.5 B 4.5 C 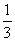D 3 　 3、如图，在Rt△ABC中， tanA=2，BC=4，则AC= ； A 4 B 2 C D 1 4、如图，在Rt△ABC中，cotA与tanA的关系是； A 相等 B 互为倒数C互为相反数D无关系 5、在Rt△ABC中，∠C=90⁰，cotB与tanA的关系是； A 相等 B 互为倒数C互为相反数D无关系	学生使用平台操作	反馈学生的学以致用的能力
课后拓展	1、如图（1），将一个长为a，宽为b的长方形(a＞b)沿虚线剪开，拼成图（2），成为在一角去掉一个小正方形的大正方形，则小正方形的边长为（） A B a-b C D 　 2、某同学想用5个边长不等的正方形，拼成如图所示的大正方形，请问该同学的想法能实现吗？ A 能 B 否 3、MN表示某引水工程的一段设计路线，从M到N的走向危南偏东30⁰，再M的南偏东60⁰方向上有一点A，以A为圆心，500m为半径的圆形区域为居民区，取MN上另一点B，测得BA的方向为南偏东75⁰，已知MB=400m，cot30⁰=1.732，通过计算回答，如果不改变方向，输水线路是否会穿过居民区？ <	学生阅读材料并解决问题	体现各学科的交融性