-
决策树算法在大学录取预测中的应用
普通类 -
- 支持
- 批判
- 提问
- 解释
- 补充
- 删除
-
-
一. 引言
随着互联网的发展,产生了各式各样的软件服务于人们的工作和生活,这些软件在服务过程中产生了大量的数据,基于这些数据又产生了大量新的应用场景, 特别是机器学习的应用场景如图片分类、广告点击行为预测、垃圾邮件识别、用户异常行为分析、银行征信评估、电影票房预测、网约车出行流量预测、基于用户位置的商业选址 (如 ATM 选址)、精准营销、兴趣推荐等。本文主要研究将决策树算法应用于美国某高校录取数据,采用Python语言建立决策树模型,利用决策树预测录取结果,并验证了该模型的准确率。
-
二. 决策树的含义
2.1 决策树概念
决策树( Decision Tree) 又称为判定树,是一种以树结构(包括二叉树和多叉树)形式来表达的预测分析模型。其每个非叶节点表示一个特征属性上的测试,每个分支代表这个特征属性在某个值域上的输出,而每个叶节点存放一个类别。
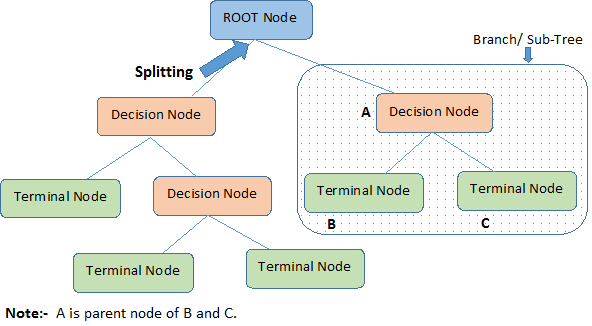
与决策树相关的一些基本术语:
- 根节点(Root Node):代表整个总体或样本。
- 分裂(Splitting):将一个节点分成两个或多个子节点的过程。
- 决策节点(Decision Node):当一个子节点(sub-node)进一步分成子节点时,我们称这个节点为决策节点。
- 叶子/终端节点(Leaf/Terminal Node):不再分裂的节点称为叶子或终端节点。
2.2 类型
决策树的类型取决于我们的目标变量的类型。共分为两类:
- 分类型变量决策树:目标变量为分类型的决策树,称为分类型变量决策树。
- 连续型变量决策树:目标变量为连续型的决策树,称为连续型变量决策树。
-
三. 决策树相关算法
在决策树模型构建过程中需依托相应的决策树算法,其主要包括ID3、C4.5、C5.0、CART 四种。
3.1 ID3算法
ID3算法在选择根节点和各内部节点中的分支属性时,采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性,在有些情况下这类属性可能不会提供太多有价值的信息.并且ID3算法只能对描述属性为离散型属性的数据集构造决策树。
3.2 C4.5算法
C4.5算法用信息增益率来选择属性,可以处理连续数值型属性,采用了一种后剪枝方法优点:产生的分类规则易于理解,准确率较高。缺点:在构造树的过程中,需要对数据集进行多次的顺序扫描和排序,因而导致算法的低效。此外,C4.5只适合于能够驻留于内存的数据集,当训练集大得无法在内存容纳时程序无法运行。
3.3 C5.0算法
C5.0算法是在 ID3、C4.5算法基础上进行改进的,C5.0算法是一种多叉树算法,在决策树生长过程中采用的是最大信息增益率原则进行决策树节点和分裂点的选择,该算法只支持解决分类问题。
3.4 CART算法
CART算法相比C5.0算法的分类方法,采用了简化的二叉树模型,其生长过程中采用的是最大基尼增益指数原则进行节点和分裂点的选择, CART 算法既可以解决分类问题也可以很好的处理预测问题。因此本研究选择CART决策树算法,作为构建决策树模型的主要算法。
-
四. 模型构建
4.1数据选择
我们基于以下三条数据预测了加州大学洛杉矶分校(UCLA)的研究生录取情况:
GRE分数(测试)即GRE Scores
GPA分数(成绩)即GPA Scores
评级(1-4)即Class rank (1-4)
4.2数据预处理
4.2.1数据清洗
(1)缺失值的处理
缺失值的处理方法主要由三种,包括删除缺失值记录;数据插补;有些模型允许出现一定量的空缺值,可以不处理。确定文件中是否有缺失值以及缺失值的属性和缺失率的个数和缺失率。
import pandas as pd
filename='"C:\Users\hy188\Desktop\student_data.csv'
data=pd.read_excel(filename)
print(data.count())
print('数据记录长度',len(data))
通过以上代码判断是否存在缺失值。
(2)异常值的处理
异常值的处理主要包含有,删除含有异常值得记录;与缺失值一样的处理方法;平均值修正;不处理。
data=data[(data[u'gpa']>=0)
print(data.count())
print('数据记录长度',len(data))
采用以上代码过滤异常数据,0分以下的数据都过滤掉。
4.2.2相关属性选择
在该数据集中“gpa”“gre”“rank”为预测列 X,“admit”为目标列y,并将数据集按8:2的比例分为训练集和测试集,其主要代码如下:
X=DataFrame(results,columns=[' gpa ',' gre ',' rank,'])
y=DataFrame(results,columns=['admit'])
X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)
4.3模型构建
本环节选择了 python 算法包中的 DecisionTreeClassifier 库进行 CART算法决策树构建,并选择了ID3算法进行对比。由于CART算法和ID3算法的区别在于划分标准不一样,CART算法将gini系数作为划分标准,而ID3算法将信息熵作为划分标准,所以我们只需要在criterion这里做一下修改就好。
(1)CART算法
from sklearn import tree
model=tree.DecisionTreeClassifier(criterion='gini')
model=model.fit(X_train,y_train)
(2)ID3算法
from sklearn import tree
model=tree.DecisionTreeClassifier(criterion='entropy')
model=model.fit(X_train,y_train)
4.4 模型可视化
根据决策树模型的训练,得出决策树模型,但是无法将决策树直观的呈现,本研究主要调用 pydotplus 包和 graphviz 图形可视化工具对决策树模型进行可视化处理,利用 pydotplus 包为 graphviz 语言提供 python 接口,从而实现 graphviz 对决策树模型可视化的一系列操作。
import graphviz
dot_data=tree.export_graphviz(model, out_file=None)
graph=graphviz.Source(dot_data)
graph.render("iris_decision_tree")
最终分别生成名为iris_decision_tree_cart和iris_decision_tree_id3的pdf文件。
4.5计算模型的准确率
利用测试集计算训练得出的模型准确率,代码如下:
model.score(X_test, y_test)
CART算法的准确率为0.6375
ID3算法的准确率为0.625
综上,在对此数据集进行训练时,选择CART算法和ID3算法的差别不是特别大,CART算法要较好一些。
-
五. 总结
本文主要利用了决策树算法对大学录取情况进行预测,选取的数据集来自美国某高校的研究生院。本文主要利用决策树中的CART算法进行模型构建,选取了‘GPA’‘GRE’和‘rank’作为特征列,选取‘admit’作为目标列。在模型构建完成之后进行了测试,得出来本模型的准确率为0.6375,准确率较高,具有较高的实用意义。
-
参考文献
[1]黄雪华.基于Python的决策树算法在学生招生录取数据中的应用研究[J].电脑知识与技术,2018,14(29):16-17.DOI:10.14004/j.cnki.ckt.2018.3368.
[2]季桂树,陈沛玲,宋航.决策树分类算法研究综述[J].科技广场,2007(01):9-12.
[3]林向阳.数据挖掘中的决策树算法比较研究[J].中国科技信息,2010(02):94-95.
[4]商惠华,戴汇川.基于Python数据分析的学业预警研究[J].电脑知识与技术,2022,18(14):22-24.DOI:10.14004/j.cnki.ckt.2022.0828.
[5]Hui Lian Han,Hong Ying Ma,Ye Yang. Study on the Test Data Fault Mining Technology Based on Decision Tree[J]. Procedia Computer Science,2019,154(C).
[6]吴俊明.ID3决策树在信息数据预测中的分析应用——以南方某高校新生录取信息数据库分析为例[J].科技创业月刊,2007(12):198-200.
-
-
- 标签:
- 决策树
-
加入的知识群:


学习元评论 (0条)
聪明如你,不妨在这 发表你的看法与心得 ~