教育数据挖掘方法与应用实验报告

实验四：对pisa数据进行logistics回归

• 理解logistic回归：通过实验了解logistic回归模型的基本概念和应用。

• 分析pisa数据：利用logistic回归分析pisa数据集，探究不同因素对学生学习成果的影响。

• 数据处理能力培养：提升数据处理、模型构建和结果解释的能力，为实际应用做准备。

• 增强理论与实践结合：通过亲自动手操作数据和应用模型，将理论知识转化为解决实际问题的能力。

• 掌握专业软件工具：学习和掌握用于logistic回归分析的统计软件或编程语言，增强实际操作能力。

spssmodeler 软件

logistic回归是一种广义线性回归模型，用于处理分类问题，特别是二分类。它通过链接函数（通常是对数几率函数）将线性预测值映射到概率空间。模型的显著性和参数的重要性通过对数似然比检验、hosmer-lemeshow检验和wald统计量进行评估。这些统计测试共同确保模型的可靠性和各变量的贡献度，对于构建准确且可解释的分类模型至关重要。logistic回归通过函数l将w’x+6对应一个隐状态p，p=l(w’x+b),然后根据p与1-口的大小决定因变量的值。

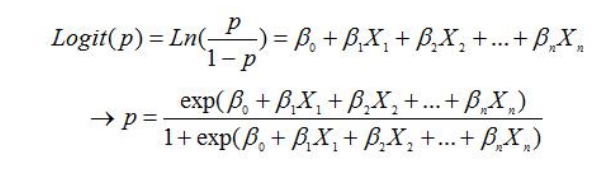
回归方程的显著性检验有对数似然检验、hosmer-lemeshow检验。对数似然检验用于假设没有引入任何解释变量的回归方程的似然函数值为l0，引1入解释变量之后，回归方程的似然函数为l1，则似然比为lo/l1比值越接近1，表明模型中的解释变量对模型整体没有显著贡献，反之则表明有显著贡献。hlosmer-lemeshow检验：如果模型整体显著，则实际值为1的样本对应的概率较高，而实际值为。的样本对应的预测概率相对较低。依据列联表得到卡方值和p值,通过比较p值和给定的显著性水平就可以判定回归方程是否整体显著。回归系数的检验wald统计量：wald检验的原假设为bi为0，wald统计量在原假设得到满足的前提下，服从一个自由度为1的卡方分布，spss將自动计算wald统计量及其对应的概率p值，通过比较第j个wald统计量对应的p值和给定的原显著性水平就可以判定第j个回归系数是否显著，当口值小于给定的显著性水平时，则认为第j个回归系数不为0，否则认为第j个回归系数显著为0。

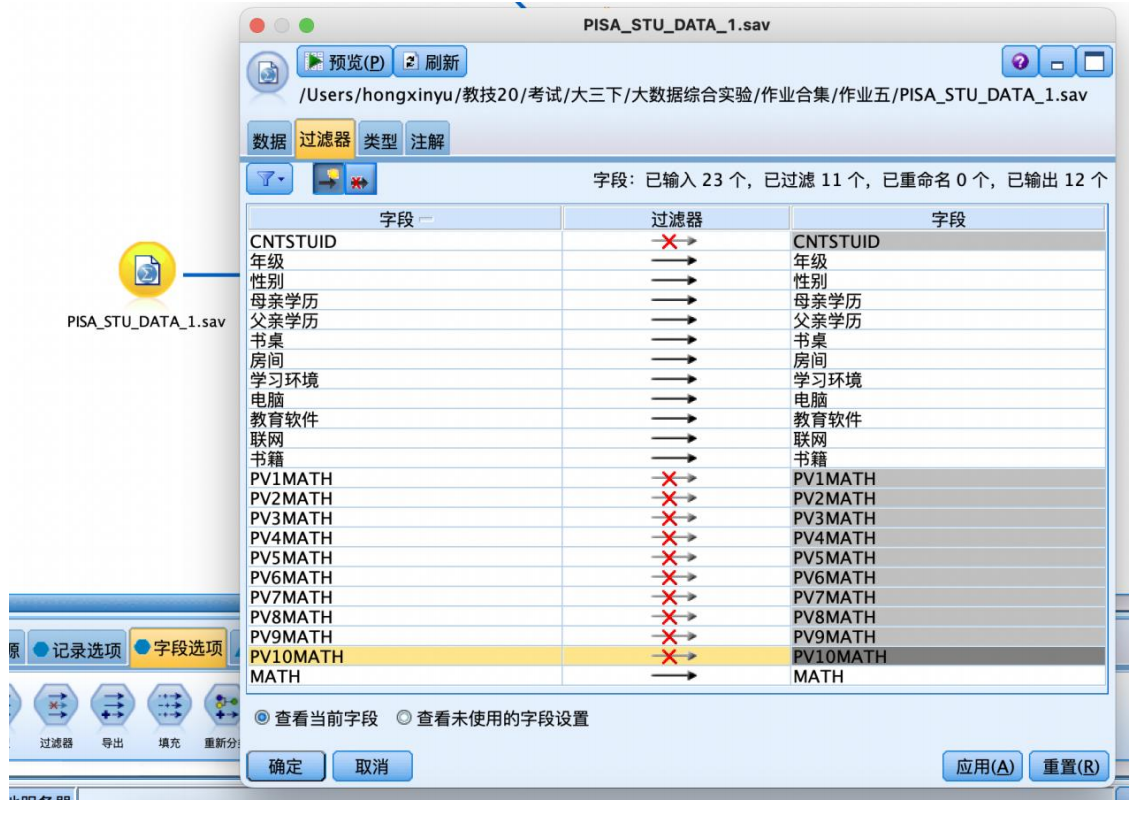
① 从“源”中拖拽出“statistics文件”到数据流编辑区，并编辑数据。设置数据节点属性，在“过滤器”选项中，过滤掉“cntstuid”字段和“pv1math”-“pv10math”这11个字段。

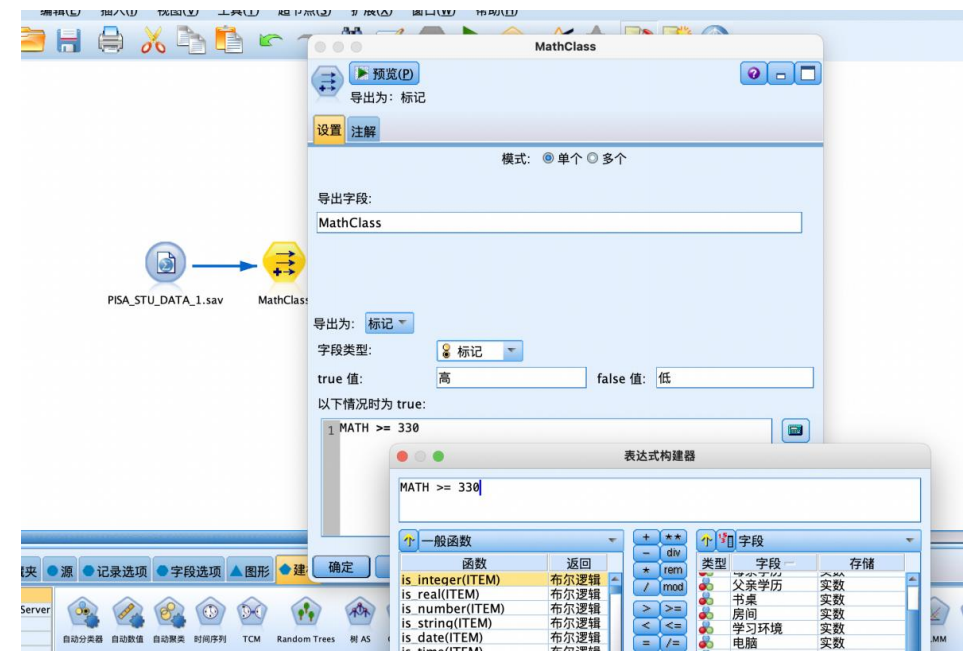
② 从“字段选项”选项卡中拖拽“导出”节点到数据流编辑区，建立连接，建立好如图数据流，并编辑“导出”节点，在导出字段框中输入mathclass，选择导出为标记，在true值框中输入“高”，false值框中输入“低”，并点击公式编辑器按钮，在弹出的表达式构建器中输入“math>=330”。

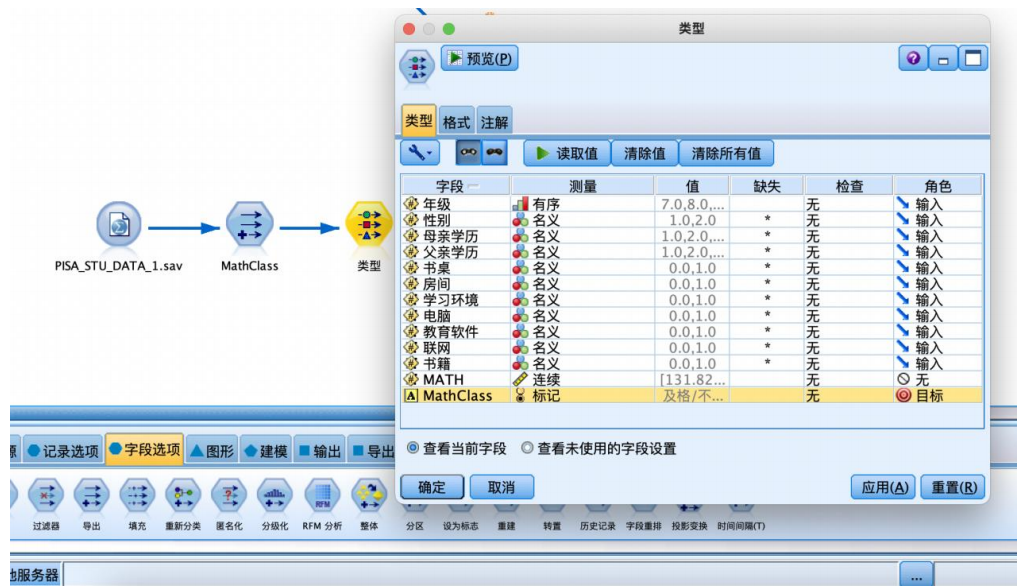
③选择“字段选项”选项卡，拖拽“类型”节点到数据流编辑区。将“类型”节点与“导出”节点建立连接，右键并对其进行编辑，将“math”字段的角色设置为“无”，“mathclass”字段的角色设置为“目标”其余字段设置为“输入”

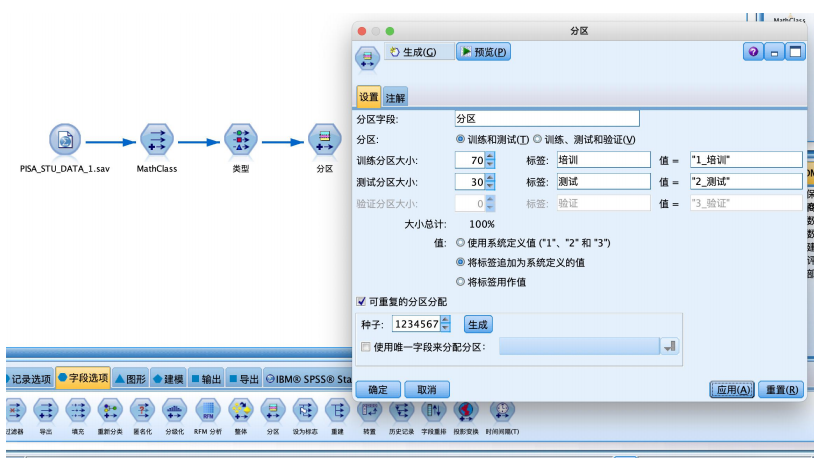
④ 从“字段选项”选项卡中拖拽“分区”节点到数据流编辑区，与“类型”节点连接，并右键编辑参数，设置70%的数据用作训练，30%的数据用作预测。

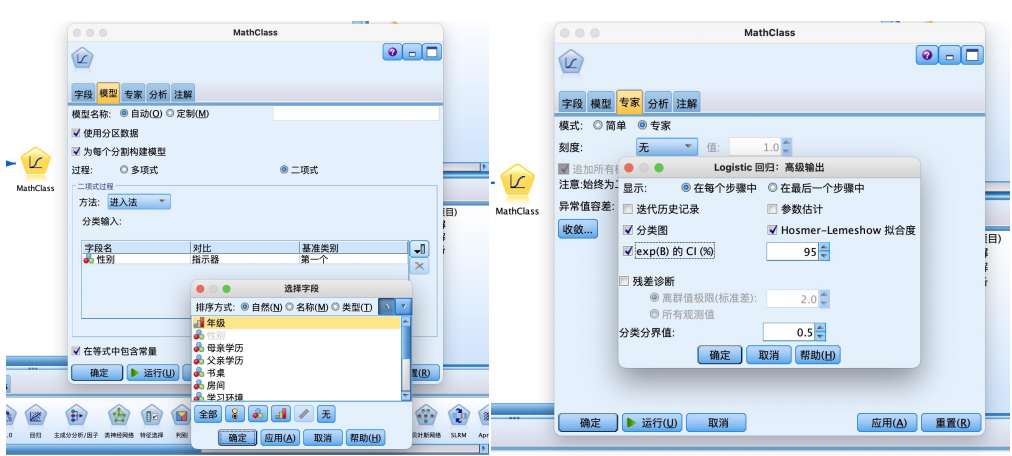
⑤建立如图所示数据流，从“建模”选项卡拖拽“logistic”节点到数据流编辑区，与“分区”节点建立连接，并进行属性的设置，在“模型”选项卡中选择“二项式”，并将性别字段输入，在“专家”选项卡中选择“分类图”“hosmer-lemeshow拟合度”以及“exp（b）的ci（%）”。运行即可得到结果。

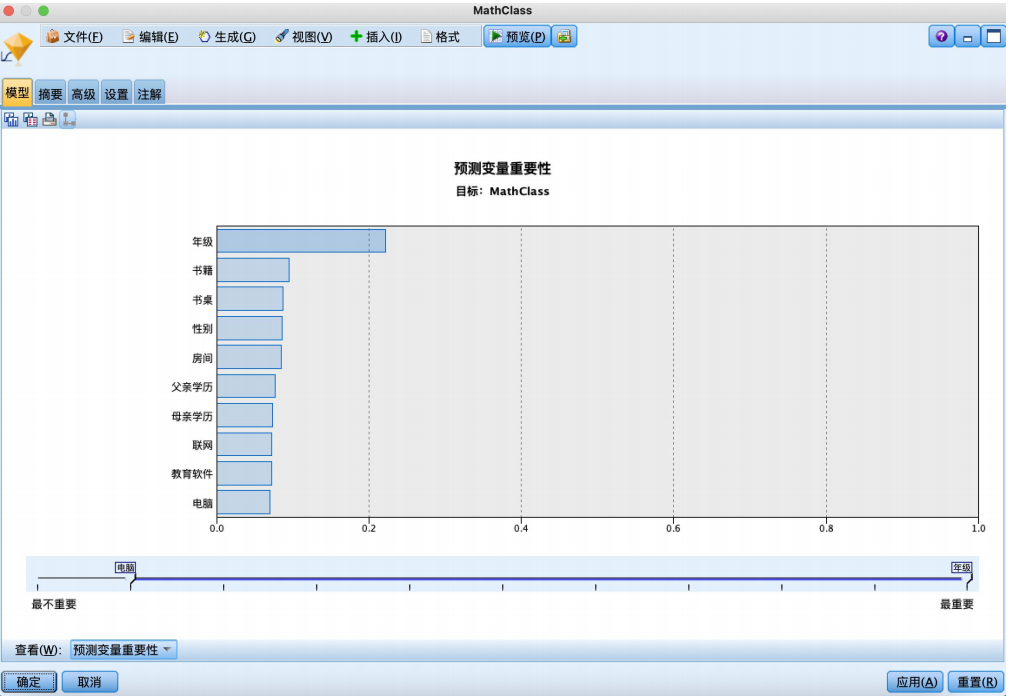
运行结果如图所示，影响学生数学成绩高低的因素按照预测变量重要性从高到低排序结果为年级、书籍、书桌、性别、房间、父亲学历、母亲学历、联网、教育软件、电脑。

成绩低的值赋为0，成绩高的值赋为1

如图为分类变量编码效果，七年级赋值为（1，0，0，0，0）可以此类推。

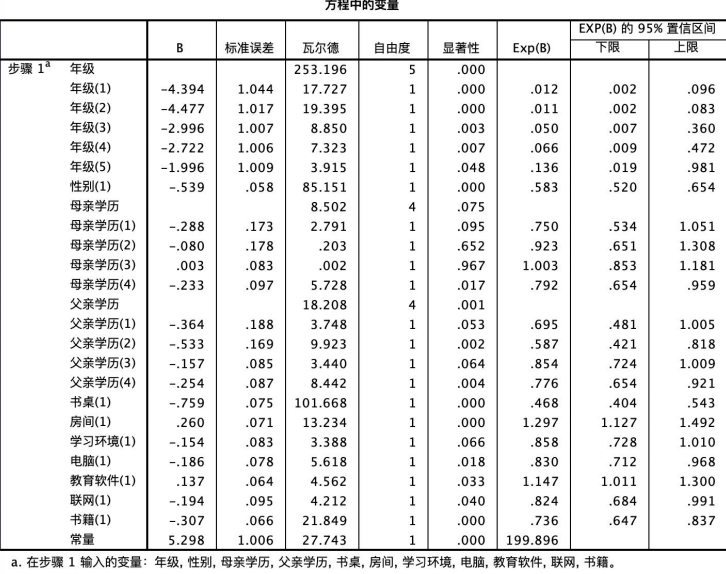
方程中的变量表格结果如图所示，可见只有常数项纳入了模型的结果，且显著性为0.000< 0.05，即存在显著性差异。

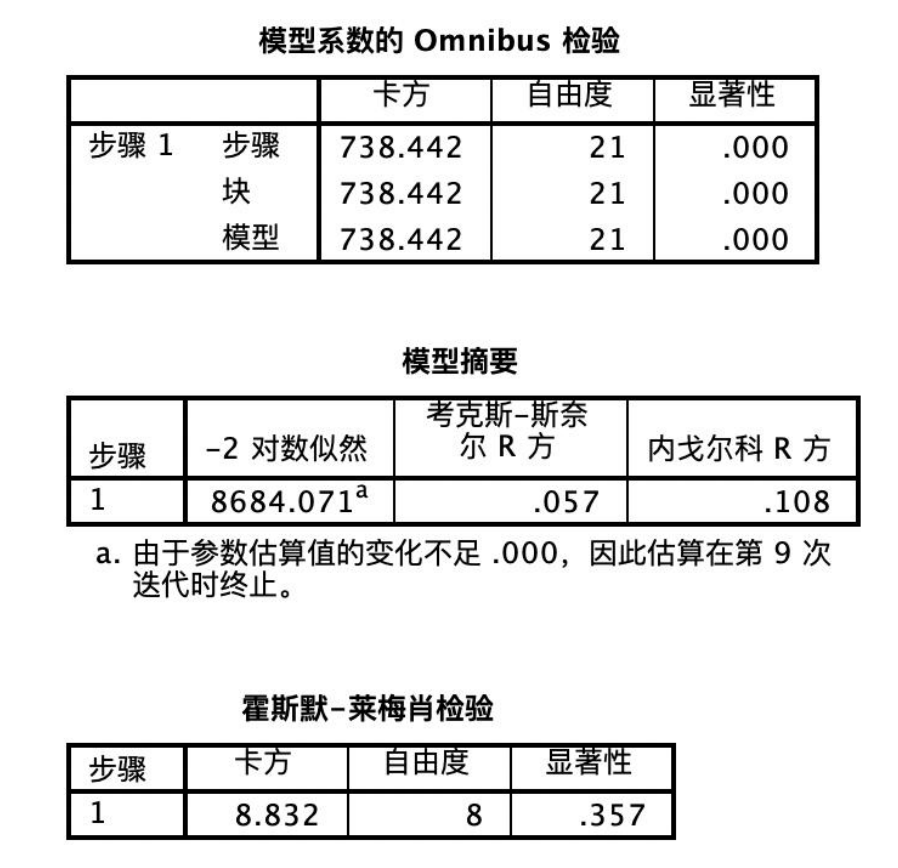
模型系数的omnibus检验结果如图所示，似然卡方检验的观测值为738.442，自由度为21，显著性值为0.000<0.05，认为所有回归系数不同时为0，输入的变量与logitp 之间的线性关系是显著的，由此可得该模型是合理的；

从模型摘要表中可得，-2对数似然值较大，该值越小说明模型的拟合度越好，因此该模型的拟合优度并不理想，而考克斯-斯奈尔r方和内戈尔科r方的值越大越好，而实验数据较小，也同样证明该模型的拟合优度并不理想。

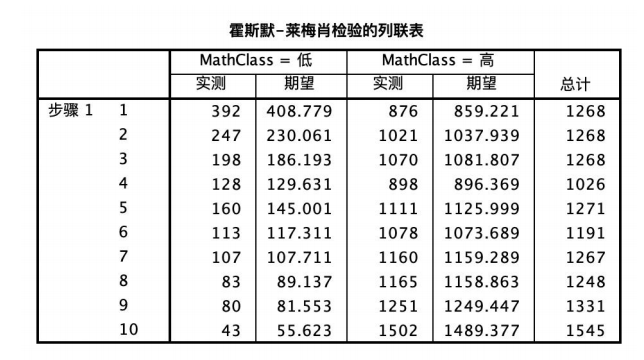
霍斯默-莱梅肖检验的结果如图所示，显著性值为0.375>0.05，不存在显著性，说明该模型拟合程度较差。

霍斯默-莱梅肖检验的列联表结果如图所示，从表格中可以清楚的读取每一组的实测值与期望值，因此可以直观进行比较，更好地判断模型的优劣。

方程中的变量相关参数的值如图所示：以性别为例，本例中以变量的第一个值为参照对象即以性别女为参照对象，则男生成绩高的概率是女生的0.583倍，且显著性值为0.000<0.05，结果显著；以年级为例，第一个值为1即七年级为参照对象，则十二年级的学生成绩高的概率是7年级的0.136倍，且显著值为0.048<0.05，结果显著。

在进行logistic回归分析后，我们得出了一系列关于影响学生数学成绩高低的重要结论。以下是对这些结论的详细总结：

1.预测变量重要性排序：

通过分析预测变量的重要性，我们发现对学生数学成绩的影响按重要性从高到低排序如下：年级、书籍、书桌、性别、房间、父亲学历、母亲学历、联网、教育软件、电脑。这表明学生的年级是最重要的因素，其次是与教育相关的物品和性别。

2.成绩编码：

我们将成绩高低分别编码为1和0，以便进行logistic回归分析。这种编码使得我们能够比较不同因素对学生成绩的影响。

模型拟合度：

分析模型拟合度的结果显示，模型中只有常数项具有显著性，而其他变量的显著性较低。这表明我们的模型在解释学生成绩方面并不理想。考克斯-斯奈尔r方和内戈尔科r方的值也相对较小，进一步表明模型的拟合度有待改进。

4.omnibus检验：

omnibus检验结果表明，回归系数不同时为0，而且输入的变量与logitp之间的线性关系是显著的，这表明模型是合理的，但并不一定适用于数据。

5.霍斯默-莱梅肖检验：

霍斯默-莱梅肖检验的结果显示，模型的拟合程度较差，因为显著性值为0.375，大于0.05。这意味着模型不能很好地拟合实际数据。

6.变量相关参数：

分析变量相关参数的值时，以性别和年级为例，我们发现性别男生成绩高的概率是女生的0.583倍，且具有显著性，而十二年级学生成绩高的概率是七年级的0.136倍，同样具有显著性。这些结果提供了有关不同因素如何影响学生成绩的详细信息。

综上所述，通过logistic回归分析，我确定了影响学生数学成绩的关键因素，并发现模型的拟合度有待改进。这些结论为进一步研究和改进教育体系提供了重要的参考信息，以帮助学生取得更好的数学成绩。

在完成这项实验过程中，我进行了一系列与logistic回归分析相关的工作，以探究影响学生数学成绩的关键因素。以下是我的实验总结与个人反思：

实验总结：

在这个实验中，我们首先收集了关于学生数学成绩以及与之相关的多个因素的数据。然后，我们进行了logistic回归分析，以确定哪些因素对学生成绩有显著影响。通过多个步骤的分析，我们得出了以下关键结论：

1.预测变量的重要性排序：我们发现年级、书籍、书桌、性别、房间、父亲学历、母亲学历、联网、教育软件、电脑等因素按照重要性从高到低排序。这为我们提供了一个框架，用于进一步分析这些因素如何影响学生成绩。

2.模型拟合度：我们的分析表明，模型的拟合度并不理想。虽然模型的一些方面表现出显著性，但仍然有很大的改进空间。这提示我们需要更多的数据或者更复杂的模型来更好地解释学生成绩的变化。

3.变量相关参数：通过分析变量相关参数，我们能够了解不同因素之间的关系。例如，性别和年级对学生成绩的影响是显著的，这为教育决策提供了有用的信息。

4.霍斯默-莱梅肖检验：通过该检验，我们发现模型的拟合程度较差，这可能是模型中未考虑的其他因素导致的。这提示我们需要进一步研究可能影响学生成绩的因素。

个人反思：

在完成这项工作时，我从中获得了一些重要的经验教训和个人反思：

1.数据质量至关重要：在进行回归分析之前，数据的质量和准确性是关键。在未来的研究中，我将更加注重数据的收集和清理过程，以确保分析的可靠性。

2.模型的选择和拟合度：这次实验提醒我模型选择和拟合度的重要性。在面对复杂数据时，选择合适的模型以及对其进行充分的评估至关重要。

3.数据解释：分析结果的解释对于研究的实际应用至关重要。我会努力提高我的数据解释能力，以更好地传达研究发现。

4.持续学习：这个实验是一个学习的过程，让我对logistic回归分析有了更深入的理解。我将继续学习和提高自己的分析技能，以更好地为我的工作提供支持。

总的来说，这次实验为我提供了宝贵的经验，使我更好地理解了数据分析的复杂性和挑战。我将积极运用这些经验，不断提高自己的技能，以更好地为教育事业提供支持和指导。