1. 了解学业成绩预测的基本概念和研究进展。

2. 掌握基于线性回归模型的学业成绩预测的基本原理。

3. 利用scikitlearn算法库线性回归模块，实现学业成绩预测模型。

1. 学习时长为6课时。

2. 在jupyterNotebook完成算法实现，并比较不同算法之间的效果

3. 搜索机器学习相关的教学视频进行学习。

4. 搜索阅读近年来关于学业表现预测的相关论文。

一、研究背景

      目前，教育行政部门、教育科研单位以及中小学正着力研究如何利用先进的预测方法，从多维度预测教育教学质量，而学生学业水平是评价教师教学效果和学生学习质量的主要指标。通过对国内外相关文献的研究发现，可以根据学习者的学习行为数据预测学生学业成绩，而学习行为特征是学情分析的基础。但是，国内目前关于学情分析的应用还局限于单纯地对学生的考试成绩等已有结果进行分析，没有结合学生学习过程中的相关因素对学生学情进行分析。本章节通过案例导入介绍学业成绩预测的相关技术原理，旨在让学生了解学业成绩预测的过程机制。

二、研究现状

      国外关于学业成绩预测的研究非常多，研究时期也比较早，从 2000 年开始，关于学业成绩预测的定量研究就已经开始大范围开始。学业成绩预测，需要依靠多学科来支持，特别是计算机科学与数学挖据技术，由于国外发达国家互联网发展比国内要早，关于这方面的研究自然要早些。国外的教学环境与国内的教学环境有很大区别，在国内，基础教育阶段，大多数采用的是传统的教学环境，利用信息系统较少。然而国外的基础教育已经经历了多个阶段的发展，从传统的教学环境到封闭式信息系统教学环境，再到开放式信息系统教学环境，到如今的新型教学环境如智能电脑，MOOC 等。随着教学环境的改变，教师对学生的评价方式、学生学业成绩的呈现方式都发生了大的改变。
      早在 1971 年，英国兰开斯特大学 Entwistle, N. J等就对学生的学习动机、学习方法和考试技巧与学生学业成绩的关系进行研究。他们以 898 名大学生、562 名师范学院学生、190 名专职学院学生为研究对象，建立数据样本，通过多种心理学量表和标准化考试对这些学生进行测试，获得相关数据，根据这些心理学指标和测试成绩分数，分析他们之间的相关性，从而预测学生的学业成绩，对学生的学业成绩预测比较精准，达到了预测目的，为教师进行教学提供了很好的帮助。国外关于学业成绩预测的研究 20 世纪前期主要是基于传统的教学环境，研究对象大多是对高校学生进行相关研究。后期随着教育环境的改变，相关研究逐渐增多，研究对象层次也逐步扩大。随着计算机科学的发展，数据挖掘技术的不断更新，在教育领域的研究也更加深入，研究方法和手段变得多样化。

       国内关于“学业 成绩”的研究相对国外并不多，研究的时间比较晚，从 2010 年才逐渐增多。我国最早开始对学业成绩进行研究的是李以渝，李以渝用蒙特洛卡方法模拟出概率模型中的随机变量，确定出各科成绩的分布以后，通过这些分布进行预先预测，然后模拟出高考成绩分布后进而定出录取分数线，能利用数学模型预测出学生的高考成绩在当时对高考招生工作来说是一个重大的进步。
       国内关于“学业成绩”研究主要是研究“学业成绩”的影响因素，例如：学业成就、学业情绪、自我效能感、学习策略、成就动机、学习动机、学业评价、家庭社会地位等。易芳等认为中小学学生学业成绩的影响因素中有六个因素相关程度最大，其中学习动机和自我效能感对学业成绩的影响最大。姜涛认为学业成绩的影响因子有 34 个之多，例如学习信心、教师鼓励等，还发现 10 个学业成绩预测因子。
       国内关于学业成绩预测的研究主要可以包括两大类：第一类是对学业成绩预测的定性研究，第二类是对学业成绩预测的定量研究，通过建立预测模型来对学业成绩进行精准预测。
      第一类对学业成绩预测的定性研究并不多，陈楠从心理学角度，在定性程度下，研究了显性自恋和隐性自恋与学生学业成绩的关系，陈玉佩通过对自我效能感的研究来预测学生学业成绩。
      第二类对学业成绩预测的定量研究相对较多。尤佳鑫等对学生在云学习平台积累的多种属性和过程性数据进行分析，建立了多元回归模型，并对在校大学生的学业成绩进行预测，并根据影响学生学业成绩的因素对学生进行教学干预。通过有针对性的教学干预，取得了较好的效果。罗敏等通过对空军招收飞行员的多项心理认知能力进行测试，并将测试分数与这些学生的高考成绩进行相关分析，建立多元回归模型。利用多元回归模型来预测未来空军招收飞行员的高考成绩。闻是之等基于对学生在一段时间内的测试成绩，运用灰色系统理论，建立了学业考试平均成绩的预测模型。综上可知，国内关于学业成绩预测的研究尽管也有不少，但是相较于国外，国内的研究时间相对较晚，研究的领域也都是对国外研究的跟进，通过学生以往的学业成绩数据来分析预测学生后续学习的学业成绩的研究则相对较少。

三、结论

       学习者学业成绩的预测和评价是全世界教育研究者共同关注的话题，而在线教育的快速发展又赋予它新的使命，即如何对在线学习者的学业成绩进行预测，以便及时提供预警和其它干预措施。而在当今网络在线学习教育快速发展的时代背景下，学生在网络教育平台上积累多特征属性数据信息，记录学习者的在线学习行为数据并加以分类，对研究学生学习成绩预测具有重要意义。

       综上所述，学业成绩预测还存在以下两方面的问题：

（1）研究数据单一；目前关于学生学业成绩影响因素的研究仅仅是寻找一类因素，只是片面的考虑当其他因素相同的情况下，被研究的因素对学生学业成绩的影响，没有对学业成绩影响因素的整体性加以考虑。另外，目前关于学生成绩预测方法的研究中，多数是以学生成绩为主题，以相关统计数据为指标进行成绩的预测，或者将前置课程的成绩作为预测指标来预测后续课程的成绩。这样做有虽然有时候会得到不错的预测结果，但是仅仅由成绩因素来预测判断学生将来的学业水平变化情况是不科学、不全面的，没有通过德智体美劳全方位的考虑到学生的学业情况。

（2）缺乏较为全面、系统的学业成绩预测模型。可以看到该领城的预测算法从 传统的统计学习方法过渡到了使用更为强大的机器学习算法，然而，其对成绩预测模型的构建较为单一，也并未出现较为可靠的、可移植手其它数据样本的方法或模型。

3.2.1 问题描述和定义

       假设给定 m 位学习者的历次模拟考试成绩数据（或MOOC平台的学习行为数据），每位学习者的数据由 n 个属性值（即 n 次模拟考试成绩）构成，可以用列向量表示第 i 位学习者的数据为 x_i=(x_i1;x_i2;…;x_in)。学业成绩预测的目标是根据学习者历史行为数据预测其最终的学业成绩表现。因此，可以构建线性回归模型进行预测，该函数表达式为：

f(x_i) = w₁x_i1 + w₂xi₂ + … + w_nx_in + b

可以用向量方式写成：

f(x_i) = w^Tx_i + b

其中 w 为行向量，可表示为 w=(w₁,w₂,...,w_n)。机器求解学习之后得到w和b，模型就得以确定。

3.2.2 数据分析及可视化

        附件中 math_percormance.csv 提供了某班级100名中学生11次数学考试成绩记录，其中前10次为模拟考试成绩，第11次（T11）为中考考试成绩。表1显示了该表的前5行数据。通过对100位同学的11次成绩作相关性分析（见表3-2）可知，T11与其他成绩相关性较高，T11与T9相关性最高，且从图3-1可以看出，T11与T9、T8之间呈现线性相关。结合表3-2和图3-1，可以尝试构建线性回归模型，用于预测学生的学业表现。

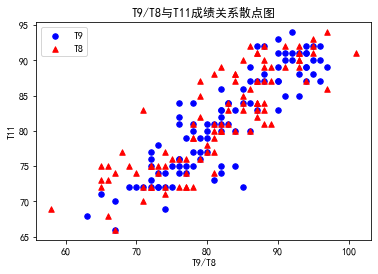
图3-1 T9/T8与T11散点关系图

3.3.1 线性

线性回归模型中的“线性”要区别于线性函数中的“线性”，这里的线性不是自变量与因变量之间的线性关系，而是因变量y对于未知的回归系数（β₀、β₁、…、β_k）是线性的，即参数线性性。如公式3-1与公式3-2是线性回归，公式3-3为非线性回归。

3.3.2 回归

回归的英文术语是Regression，这个词是由达尔文的大表弟高尔顿爵士(Sir Francis Galton，1822-1911)提出的。身为英国皇家学院院士，维多利亚时期的统计学家、社会学家、人类学家、心理学家、优生学家、非洲探险家、地理学家、发明家、气象学家计量心理学家和指纹之父，高尔顿爵士对智力非常感兴趣，作为孕育了多位杰出人才的大家族的成员之一，他想证明天赋在家族中是代代相传的。他煞费苦心的收集了605名英国名人上溯400年的家谱数据，研究结果令他失望：这些名人的父亲和儿子并没有他们那么优秀；同时，他发现，收集身高数据比判定人的优秀程度要容易很多，而且遗传性更强，于是他把研究目标转到了身高上。他发现：

      （1）高个子父母的儿子身高往往也比普通人高，但是没有他父辈高；

      （2）矮个子父母的儿子身高往往也比普通人矮，但是没有他父辈矮。

        他称这种现象为复归或回复（reversion），后来改为"回归平庸"（Regression towards mediocrity)。在高尔顿父子问题中，他发现身高的预测值都在一条直线附近（图中OM，O坐标原点，M大约2点半方向），其斜率要比椭圆的长轴的斜率要小，数值大约是0.5，这意味着父亲身高每增加1英寸，儿子的身高平均增加0.5英寸，他称这条线为回归线。

        简单来说回归就是基于已有数据对新的数据进行预测，预测的值如果是连续值那么该任务为回归任务。与回归相对的是分类问题（classification），分类问题要预测的变量y为有限的离散值，预测值只能是有限集合内的一个。当要预测的变量y输出集合是无限且连续的，我们就称之为回归。比如，天气预报预测明天是否下雨，是一个二分类问题；预测明天的降雨量的多少，就是一个回归问题。

3.3.3 线性回归

线性回归主要用来解决回归问题，也就是预测连续值的问题。而能满足这样要求的数学模型被称为“回归模型”。最简单的线性回归模型是我们所熟知的一次函数（即 y=kx+b），这种线性函数描述了两个变量之间的关系，其函数图像是一条连续的直线。

        还有另外一种回归模型，也就是非线性模型(nonlinear model)，它指因变量与自变量之间的关系不能表示为线性对应关系(即不是一条直线)，比如我们所熟知的对数函数、指数函数、二次函数等。

         现在我们知道“线性回归”就是利用线性模型来解决“回归问题”，那到底什么是回归问题呢？你可以把它理解为“预测”真实值的过程。在《三国演义》中有一个非常精彩的片段“七星坛诸葛祭风”说的是诸葛亮借东风的故事。抛开历史，单从科学角度出发，诸葛亮借东风就是一个“回归问题”。首先诸葛亮需要掌握大量的天文地理知识，并凭借自己的知识对以往的天气数据进行大量研究，最后才能预测某个时间将有“东风来临”。这种相似的回归问题，在实际生活中我们经常遇到，比如根据历史行情预测股票走势、预测房屋售价以及电影票房预估等等，而要实现这些预测就需要大量的“历史数据”作为支撑点。

         在上述讲解过程中，“预测”与“历史数据”被反复提及，既然是预测，那么就不能说它是百分之百精确的，所以线性回归只是无限地逼近“真实值”，而这个逼近的过程需要大量“历史数据”提供支持，因此线性回归就是利用线性模型来“预测”真实值的过程。

3.3.3 多元线性回归原理

第一步：构建模型。以某班中学生数学成绩预测为例，其线性回归模型为 f(x_i) = w^Tx_i + b。

第二步：构建目标函数。目标函数指XXXXXXXXXX。多元线性回归的目标函数为公式3-4。

1.大家对学业成绩预测有什么新的认识？

[1]陈子健,朱晓亮.基于教育数据挖掘的在线学习者学业成绩预测建模研究[J].中国电化教育,2017(12):75-81+89.

[1]冯广,罗时强,陈卓,江家懿,伍文燕.基于在线学习行为数据的成绩预测方法[J].中国教育信息化,2022,28(08):86-94.