《生活中得轴对称》是以“对称”为主题，试图使学生通过这样一个具有明显数学指向的概念作深刻的数学理解，在此基础上，将对称的概念拓展到艺术、科学、生活等各个领域，力图使学生呈现一种对“对称”概念的延展性、动态性的理解过程。学生学习“对称”概念，不仅仅是一个知识理解、建构的过程，更是一个依托“对称”，获得对数学、科学、艺术等各领域的文化认同与感受，并进而使学生建立对各领域之间的联系、交融的深刻感悟。因此，在进行《生活中得轴对称》教学资源设计时，我们将资源按其在课程中的功效分为感受对称、对称的数学化理解、对称的拓展性理解。
　　感受对称主要是以导入课、小组分头设计、作品展示等形式展开，引发学生对“对称”的前概念以及个人的真实理解，激发学生的内在深层次的学习渴望、好奇心、探究欲。在导入阶段，以生活中的住房选择为引子，创设观察图片（剪纸、雕塑、亭子、脸谱、牌坊、桥）情景，让学生初步形成关于“对称”的感性认识。

 
　　在小组分头设计、作品展示阶段，让学生通过讨论、交流，并利用画图、几何画板等软件，自己动手制作一件关于对称的作品。

 
　　通过这样的教学方法和教学资源设计，促进学生运用“头脑风暴法”对“对称”概念的理解。比如，有的学生通过人体造型摆出对称的汉字、对称的英文字母等；有的学生通过小品中的语言等表达对对称概念的理解；还有的学生自制包含对称的美术图案，并表达一个明确的主题；还有的学生展示一张图片，并就对称性主题对图片进行分析。
　　感受对称的教学资源设计思路是：通过大量的活动分析学生对对称概念的前理解，分析学生对“对称”这一主题的思维结构究竟是什么样的。跟踪学生的整个活动、设计、展示过程，教师要对设计小组给予各种支撑、帮助，尽可能借助直观、动作，使学生能多元化地表征对称概念。
　　对称的数字化理解主要通过各种活动，渗透对“对称”各种类型（轴对称图形、两个图形轴对称）、特征的学习与理解，并试图拓展到将对称作为一种思想方法的理解。

 
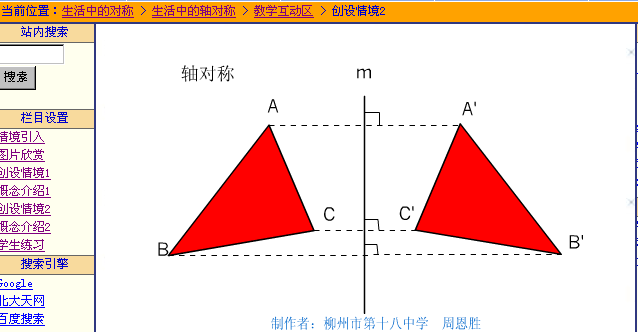
　　用动画演示说明两个图形轴对称的特点，有利于学生对对称类型的鉴别，有利于师生这个学习共同体之间通过对话、协商、合作、交流，对“对称”的性质进行提炼和实践运用。例如看到上述演示后，教师用“请一个同学说出在图形的翻折过程中，哪些量是相等的”？来引导学生把自己的体验转化成数学问题并展示给全体同学，让学生之间形成交流的氛围，在交流中受到启发。学生展示之后，教师又可以引导学生继续翻折，并要求学生把他们自己的翻折画在纸上，发现有困难的学生，可以通过小组协作或个别指导的方式帮助学生从交流中获取有用的信息，从而促进师生、生生之间共同提高。
　　对称数学化理解的教学资源设计思路是：让学生在体验和交流的活动中进行学习，从而使教师能够关注课堂上学生对对称理解上的各种明显与细微的变化，引发学生对知识的共同认识，从而达到本节课的教学目标。（1）在知识与技能方面，通过动手实践，学生能归纳出轴对称图形的性质，理解轴对称图形是一种特殊性质的图形。通过结合对比轴对称图形的性质，学生能总结归纳出两个图形的轴对称的性质，理解并深刻体会轴对称图形和两个图形的轴对称之间的区别和联系。

（2）在过程与方法方面，学生经历探索轴对称性质和图案设计等实践活动，进行有创意的设计、初步掌握利用轴对称性质进行具有象征性意义的图案的设计与制作。通过大量的做一做，想一想，试一试等教学活动，使学生体会所学内容与现实世界的广泛联系，体会轴对称的数学内涵和文化价值，积累丰富的数学活动经验，发展良好的空间观念和一定的创新意识。同时大量的学生活动，给学生提供了探索与交流的时间和空间。在学习过程中，学会与同伴交流与他人合作。（3）在情感与态度方面，通过欣赏生活中（包括艺术作品）的轴对称图形，了解图形在生活中的多含义表达，体会轴对称图形是现实生活中有较高使用价值的图形，并通过图形的对称美来感受数学美。
　　对称的拓展性理解是将对称主题渗透进物理、化学、生物、艺术、生活等各个领域之中，使学生借助数学的理解，深刻认识其他领域中的对称现象，试图依托对称，让学生感受到数学是与科学、艺术、生活等紧密联系的，并发自内心地感悟到数学本质上是一种深刻的人类文化，促进学生对数学的高层次理解。

 

　　拓展性理解的教学资源的设计思路是：通过查找并阅读资料、讨论研究、游戏竟猜等形式，引导学生主动探索、合作探究。具体内容涉及：化学中的晶体结构的对称性、建筑物的对称性、对称与运动、对称与不对称等。

 
通过跟踪研究、记录体会，并反复观摩与分析现场实拍的各种录像资料，设计和实施《生活中的轴对称》主题式教学资源，对于学生关于数学概念的深层次理解有着极大的促进作用，学生已经开始对某些较前沿的科学概念有模糊、朦胧、初步、粗浅的意会与认识。比如，学生甲在大屏幕投影上展示了一棵树，并向学生乙发问：“请问这棵树是对称的吗？”学生乙说：“远看是对称的，因为左右两边看似一样，但近看由于每个树杈、每个树杈上的树叶不相同，所以又不是对称的。”这一问题已体现出学生实际上开始接触到分形学的一些核心思想，即在第二级、第三级……意义下的图形的变化。