1.了解mooc辍学行为的基本概念，与辍学行为产生的背景

2.理解RNN算法，以及正向传播与反向传播

3.理解GRU模型

1.建议学习时长为6学时；

2.学习之前可以先阅读相关文献，了解MOOC辍学预测的相关案例；

3.尝试利用RNN和GRU模型对MOOC辍学进行预测。

         MOOC因其资料共享型、课程开放性、教育自主性和终身性等传统教育行业欠缺的优质特色吸引了全球数以万计的学习者加入。此外它不受时空限制的特性，实现了以学生自学为主的学习形式，更充分的利用优质的教学资源，并且为学生提供了专业且个性化的学习服务，这是一种教学方式，更是一个完整、全面的教学系统。但同时也因其自主选择性而导致极高的辍学率，成为制约MOOC普及和发展的主要原因。

  随着慕课的发展，平台注册的学生，可提供的课程逐步增多，课程列表里面出现了许多相似的课程,这就造成了学生难以找到合适的课程,进而出现了因为学习过程中才发现不合适而放弃继续学习的情况。高翘课率、低通过率影响了慕课的进一步发展，想要解决上述问题，需要充分掌握学习者日常的学习行为，利用RNN、GRU模型对学习行为数据进行统计分析，对是否辍学进行预测。

MOOC，大规模开放在线课程(Massive Open Online Course) ，是一种全新的教育模式，是“互联网+教育”的产物。作为一种在线学习环境，学习者可以免费访问、注册和在线学习，不再受时空、个人教育背景的限制，随时随地学习北京大学、清华大学、甚至是东京大学、新加坡国立大学、哈佛大学、剑桥大学等世界范围内知名学府开设的课程，接受权威专家直接指导，MOOC平台为学生提供了学习高质量课程的机会。中国传统教育一直存在资源分布不均、投入产出失衡、素质教育水平较低等困境，因此MOOC的出现对革新传统教育模式提供了无限可能，是对传统教学模式的一次“颠覆”。慕课这一概念自2008年被提出后，2012年还有Coursera、Udacity、edX三大国际平台的推出，慕课进入了高速发展的快车道，在世界范围内如潮水般得到推广。后面又相继出现了中国大学MOOC、Stanford Online、NovoED、FutureLearn、学堂在线、酷学习等一大批国内外的MOOC教育平台，为学习者提供包括历史、人文、计算机科学、生物学等多个学科的课程。 随着互联网技术的快速发展，以MOOC为核心的教育平台吸引了数以亿计的学习者在线上学习和交流。在MOOC学习平台中，学生现如今不仅可以自由的访问课程视频，完成作业和参加考试，还可以使用在线论坛和维基等辅助工具。另外由于现在新冠疫情的刺激，MOOC平台的作用越发凸显。但是，在学习者数量激增的表面繁荣之下，MOOC学习也出现了质量上的“学习危机”。由于师生缺少面对面交流，学生上课时间碎片化等问题，MOOC学习具有极高的辍学率。相关研究表明，大多数在线学习平台的课程完成率低4%-10%，而辍学率高达80-95%。并且MOOC学习环境中教师相比于学生数目较少，教师无法跟踪每一位学生的学习行为。因此，对学生进行精准和及时的辍学预测，从而提高MOOC平台课程的保留率，改善MOOC课程质量和教学方法对在线学习的持续健康发展具有重要意义。

        高辍学率对MOOC平台和学生自身都有负面影响，不利于MOOC在全球的持续发展。从平台角度看，辍学会增加每个学生的平均成本，因为吸引新学习者的注册成本远大于留住潜在辍学者的成本。而从学生角度来看，辍学是对时间和精力投入的浪费。为了解决高辍学率这一显著问题，就必须充分利用MOOC平台中记录储存的海量学习者行为数据建立预测模型，实现对辍学者的精准预测。辍学预测是根据学生历史学习行为记录来预测未来某个时间推出课程的可能性。通过对学生行为建模预测辍学概率，可以随时获取学习者在平台的学习情况，提前发现其辍学风险。MOOC平台存储的学习行为数据主要包括点击流数据、论坛数据和作业数据三大类，研究者通过制定合理的特征工程从这些行为数据中提取影响学生最终学习效果的特征，以便进一步建立辍学预测模型。其中点击流数据因能较完整地反映学生的学习轨迹，在构建辍学预测模型时往往能取得较好的性能。

       现有的辍学预测方法主要使用传统机器学习算法和深度学习算法建立预测模型，从而提高预测的准确性。国外学者在关于辍学模型预测领域进行了很多充分的研究并取得了一定程度的成果。Lakkaraju运用逻辑回归、 随机森林、 Adaboost 等机器学习方法来预测高中生是否能够顺利毕业。Chaplot提出使用情感度来扩展特征空间的方法， 并结合神经网络模型来预测MOOC的辍课问题。Bart Pursel等采用 logistic 回归分析为模型， 使用MOOC学习人数、 学习者论坛互动情况等学习行为数据， 通过模型训练这些数据变量来预测课程完成情况。John Z. Dillon 和 Saurabh Nagrecha 使用四种不同的分类器对同一课程中的学习者是否辍学进行预测，并根据预测结果来分析其辍学的原因。国内关于对MOOC辍学率的问题研究虽晚国外几年，但成果显著。蒋卓轩等运用3种机器学习方法对同一 时间跨段的学习行为数据进行训练来预测学习者的课程成绩并对比三种结果。王雪宇等从课程、 学习者、 平台三个方面对中美在线学习者的学习行为进行对比分析， 并指出了MOOC 等平台高辍学率的影响因素。随后王雪宇等对国防科技大学 MOOC 平台中最热门的 8 门课程进行辍学预测，选取了11种学习行为数据并对神经网络和多元线性回归模型进行性能对比。刘文彦在多个分类器的基础上提出了一种多分类器加权联合模型来预测流失率， 很大程度上提高了预测精度。 陈立德运用聚类和关联规则挖掘技术对学员的学习行为进行挖掘分析， 并使用具有长短期记忆单元的递归神经网络模型预测辍学问题。

        在对MOOC学习者辍学行为建模预测方面， 目前已有的研究成果，存在的问题比较集中的体现在两个方面。第一，在线教育问题涉及多门学科，对其进行辍学率预测需要运用教育学和计算机学的理论知识，很多研究者仅以比较单一的学术背景进行研究，对在线教育领域进行研究的系统性不够。第二，诸多研究者对辍学界定的原则均为某一时间点后的一段时间是否有日志行为。事实上，如果一段时间后仍然继续回来学习，这只是翘课行为，不再继续学习才是辍学行为。 两者性质不同， 而现有研究中均未进行有效区分。

        本章主要对“学堂在线”平台数据集进行一些处理和描述性分析，运用RNN、LSTM、GRU模型对学习者辍学情况进行预测，并分析这三种模型的预测性能，得到最优方法。

一、辍学的形成与定义
(1）辍学的形成
      MOOC学习平台中一门课程的学习时间一般不会超过10 周，在此期间平台每周都会定时定点的更新课程视频，用户可以通过观看视频、论坛交流等来进行自主学习，然而在线学习并没有类似于传统教学课堂的实时监督管理,很多用户会因为各种因素停止课程学习，辍学现象就出现了。然而平台管理者只能通过收集整理学习者的视频点击率、作业完成情况、论坛讨论记录等学习行为来了解他们的学习情况。
(2）辍学的定义
       百度百科上并没有对在线学习辍学进行专业的定义,不同学者根据各自的研究点对此采取了不同的定义。一般分为两类:一些学者注重于研究学习过程，将课程进行期间的某一段时间没有学习行为的学习者视为辍学;另一些学者将课程将要结束前的一段时间没有学习行为的学习者视为辍学。这两种定义含有一共同点，都需要运用学习者在当前课程的学习行为来提取特征、建模预测未来是否还会继续上课。
      本文采用前者的方式来定义辍学问题，由于采用的kdd cup 2015数据集的课程时间跨度为29天，这里本文为了方便分析研究，将课程时间跨度统一看成30天，在开课后的30天内，通过对学员前期学习行为的挖掘分析，预测其是否会在接下来的10天内辍学。界定的原则为在某一时间点后面10天内是否产生学习行为记录。若10天内没有学习行为归为辍学，标注为1，反之为未辍学，标注为0。

二、数据集分析
      本研究采用“学堂在线”为“KDDcup2015”竞赛而公布的数据集，该数据提供了系统的完整的在线教育数据，具有很高的研究价值。该数据集记录学堂在线平台的部分学员的选课情况和学习行为，共分为有5个文件，均为CSV格式，其中有训练集、测试集、验证集、课程信息、开课周期。由于测试集的日志记录文件并未提供样本标签，因此在本文随后的实验分析中测试集数据被剔除，仅仅采用有标签的训练集数据。
       本研究采用“学堂在线”为“KDDcup2015”竞赛而公布的数据集，该数据提供了系统的完整的在线教育数据，具有很高的研究价值。该数据集记录学堂在线平台的部分学员的选课情况和学习行为，共分为有5个文件，均为CSV格式，其中有训练集、测试集、验证集、课程信息、开课周期。由于测试集的日志记录文件并未提供样本标签，因此在本文随后的实验分析中测试集数据被剔除，仅仅采用有标签的训练集数据。
       在2014年2月份和8月份行为日志数较低，最低数量仅有492。因为国家、事业单位、校园期末等各大考试都集中在每年6月和12月左右，所以临近考试期，在线学习人数增多，学习行为日志也随着达到最高峰;随后学习者数量不断减少，学习行为日志下降的非常快，在寒暑假期间达到最低值，说明学习者大多数为学生且他们在放假后基本不参与学习。该数据集所反映的现象与实际情况相符，所以该数据集具有代表性。

RNN(Recurrent Neural Network), 中文称作循环神经网络, 它一般以序列数据为输入, 通过网络内部的结构设计有效捕捉序列之间的关系特征, 一般也是以序列形式进行输出。

RNN单层网络结构:

以时间步对RNN进行展开后的单层网络结构:

RNN的循环机制使模型隐层上一时间步产生的结果, 能够作为当下时间步输入的一部分(当下时间步的输入除了正常的输入外还包括上一步的隐层输出)对当下时间步的输出产生影响。

RNN模型的作用:

因为RNN结构能够很好利用序列之间的关系, 因此针对自然界具有连续性的输入序列, 如人类的语言, 语音等进行很好的处理, 广泛应用于NLP领域的各项任务, 如文本分类, 情感分析, 意图识别, 机器翻译等。

RNN模型图示：

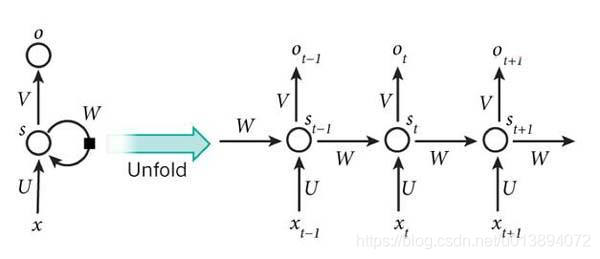
RNN正向传播：

RNN模型图示：

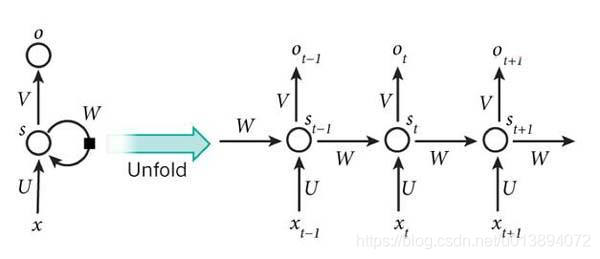
RNN反向传播：

• 数据处理

  由于学生的行为数据计数分布是非常不平衡的，所以我们要先进行归一化，这里选择的是z-score归一化，使得模型能够更快收敛。

  在本文的学生辍学模型中，数据集就是一个不平衡的数据集，经统计，我们发现目标值为1（辍学）的用例数量与目标值为0（未辍学）的用例数量比值接近4:1，其实对于所有注册MOOC课程的学生来说，还有大部分是从来没有在MOOC上产生学习行为的，学生真实的辍学概率甚至达到了90%左右。这种比较不平衡的数据集造成的结果就是我们学习到的的模型决策边界会使得多数类的分类准确率更高，但是对于少数类的信息学习到的可能并不多。

  为了削弱这种情况的影响，我们使用了一些解决数据不平衡问题的常用算法。本文采用了三类方法：在机器学习代价函数中赋予类别权重、过采样、欠采样。

  赋予类别权重：本文前面对于损失函数的定义是统一的，举例来说，本文将正类判断为负类以及将负类判断为正类的损失是相同的，然而，现实中并不是如此，由于这里少数类只有多数类的1/4左右，为了平衡两类之间的关系，我们可以适当的提高少数类损失的权重，那么最后我们得到的模型会更好地拟合少数类样本。

  过采样是指用一定的方法对类别样本数目较少的样本进行再次采样，使得两类样本的数目基本相等。所使用的方法主要是：随机过采样、SMOTE算法、bS MOTE。

  欠采样则是对多数类的样本进行随机采样，使得达到均衡状态。所使用的方法主要有：随机欠采样、Near-Miss1、Near-Miss3。

• 特征工程

  特征工程决定了最终我们的模型输入到底是什么样的，即每个用例有多少维特征，每个特征分别表示什么。这些特征直接决定了我们的模型学习效果，好的特征会对训练和测试结果带来质的提升。以下三种是经过实验之后能显著提升我们的测试结果的特征：

         1.交互特征。交互特征包括学生注册课程并在课程学习中产生的特征，分两种类别，一种是统计特征，一种是二分类特征。统计特征包括学生与课程交互的events中的七种行为的总和特征。每个交互日志学生接触的课程对象所属的种类，主要分了以下几类：sequential，problem，chapter，video，combinedopenended，以及并未在原始数据中明确命名的种类，然后是一天24小时的学习统计数据，即学生在课程学习过程中产生的行为主要是在一天的什么时间段，如学生喜欢在晚上10点之后学习，产生的行为主要集中在晚上10点到11点这个时间段，这个时间段的数值就非常大，除此之外，还有一周七天的学习频率统计数据；二分类特征就是“是”或者“不是”，如课程特征就是一个二分类特征，学生注册的是哪个课程，经过统计总共有39个课程在数据中出现，所以我们进行0-1编码之后，每个学生课程交互数据中有39维特征是0-1特征，学生注册的这个课程对应的编号特征为1，其余的都为0。其实所有的统计特征都可以表示为二分类特征，如果在统计特征中的特征值不为0，在二分类特征中就为1，反之就为0。

         2.时间特征。这里要预测的是未来10天的学生辍学情况，所以可以将时间粒度放大一些，比如10天作为一个时间的分割点，每10天学生都干了什么事情，做了多少事情。当然也可以将一周作为一个时间分割点，这样可能更符合常识。

          3.依赖特征。这种特征建立在基本特征之上，能够显著地提升我们的模型效果。

构造依赖特征所使用的聚类算法：k-means算法、GMM算法、Field-aware GMM算法。

1. “依赖”的第一层含义：“依赖”就是依赖学生或者课程自身的特点。

假设这里有一群身份、背景、性格、习惯都非常相似的学生，他们在MOOC上所表现出来的特征会有很多的相似性，这种相似性体现在他们是以某个点为中心独立同分布的生成他们的数据，那么我们必须把学生之间或者课程之间的相似度也考虑进去，这样就相当于针对性的训练某个学生集合产生的数据，训练出来的模型才会更可靠，也更准确。

2. “依赖”的第二层含义：这些特征既依赖于训练数据集，又依赖于测试数据集。

训练数据在进行训练时，因为我们知道测试数据也有很多数据与训练数据是关联的，为了表示这种关联，我们就可以构造一些训练数据和测试数据共有的特征，这些特征就可以作为两者之间的依赖关系而存在，而且在我们针对于训练数据进行模型训练时，其实考虑了部分测试数据的信息。

3. 分组依赖特征：分组依赖特征就是对于我们已有的基本特征进行分组，然后通过一定的数学运算得到最终的特征。具体过程如下图所示：

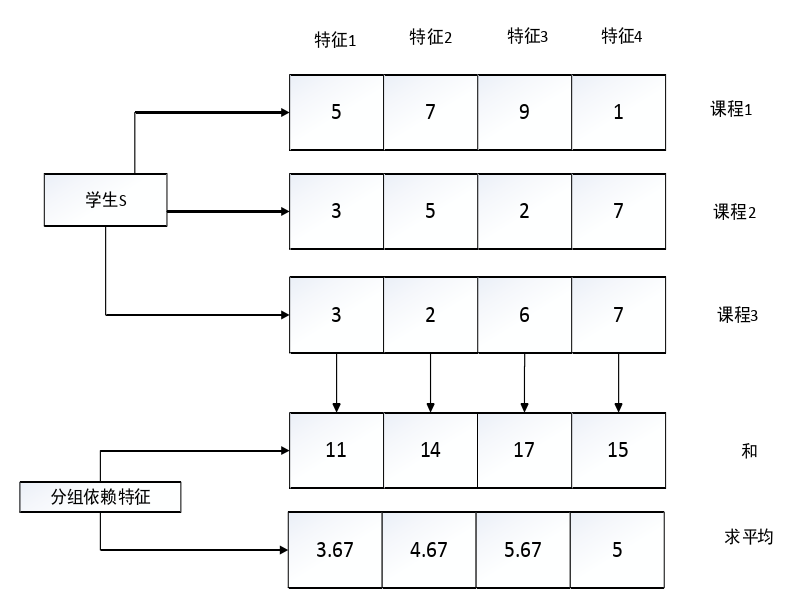
学生S在3门课程上产生的特征经过累加或者求平均之后得到分组依赖特征。此处“分组”即以学生为“组”，还有以课程为组，与其是相似的。所谓“累加法”，其实是最简单的一项处理方法，我们将同一个学生的行为数据做一个总和，得到他在各个课程中的各个行为分别总共为多少。上述“累加法”有一个缺陷就是还有很大一部分学生只注册了一个课程，那么产生的行为数据就比较少（相对与那些注册了多门课程的学生来说），那么我们就必须用“平均法”除以学生注册的总的课程数。

4. 聚类依赖特征：分别计算39门课程的所有产生数据的用户的特征（object特征）；分别对39门课程的数据进行聚类；将聚类的结果拼接起来。用聚类特征代替object的好处在于大大减小了特征的维度，并且利用了测试数据集中的数据，而且其中还包括了课程因素。

特征总结表：

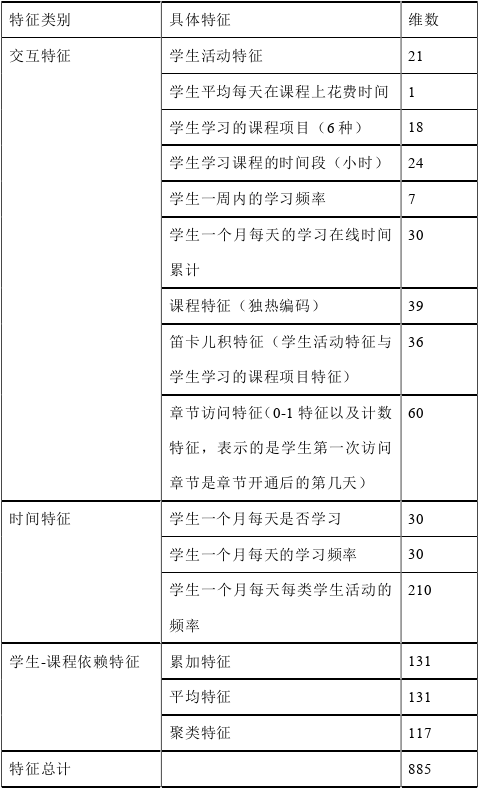
• 模型基本介绍

         1.RNN模型

  左边是未展开的RNN模型，右图是展开之后的RNN，W2表示转移权重矩阵，W1表示输入权重矩阵，W3表示输出权重矩阵。X,Y分别表示输入与输出，在本文中分别表示学生的学习行为特征，以及学生是否辍学。可以看到RNN是一个循环结构，共享了三个权重矩阵，我们首先把输入数据按时间顺序分片然后输入到模型里，之后通过BPTT算法[18]进行权重的优化。

        2.LSTM模型

        Vanilla RNN模型有一些缺点十分明显：梯度弥散。由于时间序列太长，导致BPTT算法计算梯度的过程中，梯度的量级不断变小，到最后趋近于0，反过来说就是时间点靠前的数据无法对于权重矩阵产生影响，主要是后面时间点的数据在起作用，也就是前面时间点的数据信息无法传到后面。LSTM模型[19]的提出主要是为了解决这个问题，使得信息依赖可以传导的更长。LSTM模型与Vanilla RNN的结构主要区别在LSTM Cell，它也是LSTM能够传导长时间“记忆”的关键所在。

LSTM Cell中主要结构就是三个“门”，分别是“输入门”（input gate）：it，“输出门”（output gate）：o_t，“忘记门”（forget gate）：f_t 。其中c_t表示LSTM Cell的状态（t时刻），x表示输入数据，ht表示t时刻的隐含层输出数据。t时刻LSTM Cell中各变量计算方式如下：

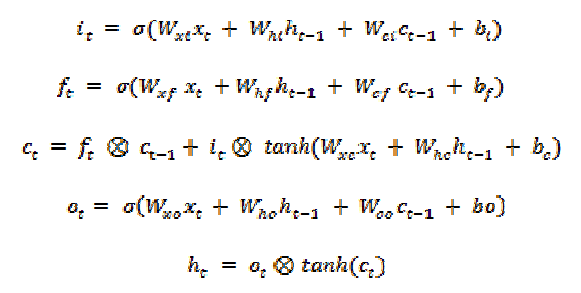
其中Ⓧ表示向量元素对应相乘。仍然用BPTT算法来进行权重矩阵的优化。

• 模型评判标准——AUC

AUC即ROC曲线下的面积，英文全称Area Under the ROC Curve，ROC即受试者工作特征曲线（receiver operating characteristic curve）， AUC是一个二分类问题的模型评判标准，ROC曲线的横坐标是True Positive Rate，即真阳率，纵坐标是False Positive Rate，即假阳率，AUC计算的就是ROC曲线与坐标轴之间围成的图形面积。AUC的意义是：随机抽出两个属于不同类别的测试用例，正类的用例在我们的模型下的预测值（属于正类的概率）大于负类用例的预测值的概率，是一个比准确率更加全面的评判标准。

• RNN模型构建

         1.RNN模型特征组成

  特征表示为timePeriod，则timePeriod1，timePeriod2，timePeriod3分别表示1-10，11-20，21-30天的用户行为特征，这里的用户行为特征包括：（1）problem_count–学生做课堂作业统计次数；（2）video_count–学生观看教学视频统计次数；（3）access_count–接触除了课堂作业以及教学视频以外的其他object统计次数；（4）wiki_count –接触课堂维基的统计次数；（5）discussion_count–接触论坛讨论的统计次数；（6）navigate_count–浏览课堂的其他信息次数；（7）page_close_count -关闭网页次数。

所以timePeriod1 = {problem_count1, video_count1, access_count1, wiki_count1, discussion_count1, navigate_count1, page_close_count1}，总共七维特征。

         2.数据集的划分

  将数据集分为训练集、验证集、测试集，数据比例为：3:1:1，步骤如下：

  （1）划分出测试集、训练集与验证集的并集，划分过程是随机的，即每个数据出现在每个数据集合的概率相等；

  （2）将训练集与验证集的并集划分为4个大致相等集合；

  （3）将（2）中产生的集合用于4-折交叉验证，确定最优超参数；

  （4）将（1）中产生的并集全部用于训练，参数用（3）中确定的超参数；

  （5）将训练出来的模型用于（1）中产生的测试集，得到实验结果。

        3.RNN模型的改进

  （1）训练过程的改进

一是想尽可能多的增加训练数据量，避免“过拟合”的产生；二是想将测试集中的信息也尽可能的考虑进去。

  （2）单层循环神经网络的不足之处

单层LSTM以及Vanilla RNN学习到的信息的时间跨度是比较单一的，为了从输入数据中学习到多个时间跨度的信息，必须改变原来的网络结构，因为第一个时间片还有第二个时间片的行为数据都可能体现出学生的某种特征，可能会影响到最后一个时间片的结果。

       （3）RNN改进1：RNN Regularization

RNN Regularization就是加上了一个dropout的处理，dropout的位置上选择的是同一时间片的节点，而各个时间片之间相连的隐含层节点有信息流动，为了让信息可以传播下去，我们必须要求他们之间是没有dropout操作存在的。而在特定时间片t内，输入层节点与隐含层、隐含层与隐含层、隐含层与输出层之间传递的信息是无需直接传播到下个时间片的，因此这些节点之间是存在dropout操作的。RNN Regularization的结构如图4-1所示，其中比较细的实线箭头表示dropout操作，黑色的粗体线表示信息的流向，也就是说信息从t-2时刻流动到了t+2时刻：

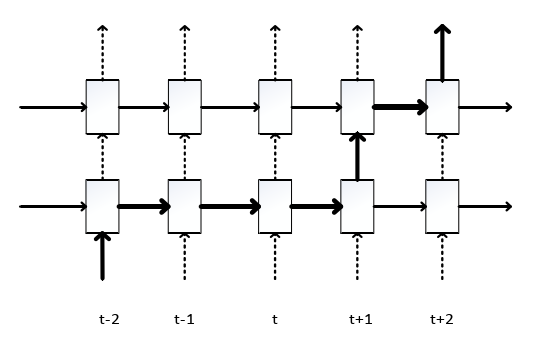
        （4）RNN改进2：Deep RNN

用Deep RNN的一种原因就是为了表示一种复杂的层次结构，单层隐含层RNN能表示的模型更简单，但是对于这种层次结构却是无能为力的；其次，Deep RNN 能够从输入中学到不同时间跨度的信息，用这种结构是为了让模型能够复杂一些，能生成多的一些隐含特征。所谓的Deep RNN就是对于普通RNN里的隐含层进行stacking。Deep RNN模型图如下所示：

4.RNN模型实验结果对比

本次实验中使用的模型有Vanilla RNN（单层隐含层）、LSTM模型（单层隐含层）、Deep LSTM模型（没有dropout操作）、Deep LSTM模型（有dropout操作）。实验结果如图所示：

 GRU（Gated Recurrent Unit）也称门控循环单元结构, 它也是传统RNN的变体, 同LSTM一样能够有效捕捉长序列之间的语义关联, 缓解梯度消失或爆炸现象. 同时它的结构和计算要比LSTM更简单, 它的核心结构可以分为两个部分去解析:

• 重置门r_t ：用来筛选信息，用Wr来控制t-1时刻每个位置输入信息的保留程度，重置门越小，前一状态的信息被写入的越少。
• 更新门z_t：用来筛选信息，用Wz来控制t时刻新、旧信息输入的保留程度，更新门的值越大说明前一时刻的状态信息带入越多。

       学生经常在连续多个时间步长内表现出相似的学习行为，即学生在第二天的学习状态有很大的可能性与学生前一天的学习状态相似，因此可通过GRU记忆模块中的更新门与重置门两个门函数对学生行为之间的时间信息进行进一步提取。更新门用于控制前一时间步长的状态信息被带入到当前时间步长中的程度，权值越大表明前一时间步长的信息带入越多，学生在相邻时间步长之下学生状态越相似，学习存在规律性；重置门用于控制忽略前度，其权值越小说明忽略的越多，学生某些偶然或无关学习行为越多。

     （1）GRU的内部结构图和计算公式

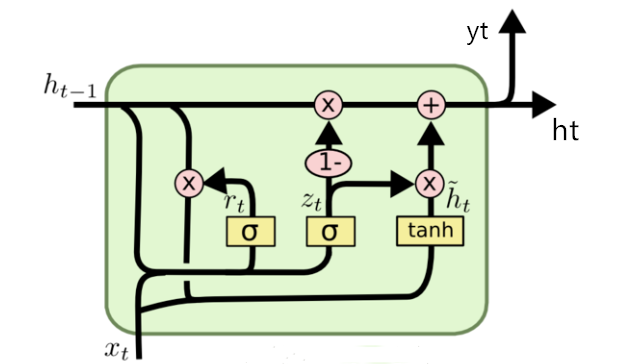
（2)内部结构分析

• 首先，计算重置门和更新门的门值, 分别是r(t)和z(t)，计算方法就是使用X(t)与h(t-1)拼接进行线性变换,
• 再经过sigmoid激活（ σ 为sigmoid函数，通过这个函数可以将数据变换为0-1范围内的数值，从而来充当门控信号）， 之后重置门门值作用在了h(t-1)上, 代表控制上一时间步传来的信息有多少可以被利用，
• 接着，就是使用这个重置后的h(t-1)进行基本的RNN计算, 即与x(t)拼接进行线性变化, 经过tanh激活, 得到新的h(t)，
• 最后，更新门的门值会作用在新的h(t)，而1-门值会作用在h(t-1)上, 随后将两者的结果相加, 得到最终的隐含状态输出h(t),
• 这个过程意味着更新门有能力保留之前的结果, 当门值趋于1时, 输出就是新的h(t), 而当门值趋于0时, 输出就是上一时间步的h(t-1)。

（3）GRU的优缺点

• GRU的优势：GRU和LSTM作用相同, 在捕捉长序列语义关联时, 能有效抑制梯度消失或爆炸, 效果都优于传统RNN且计算复杂度相比LSTM要小。
• GRU的缺点：GRU仍然不能完全解决梯度消失问题, 同时其作用RNN的变体, 有着RNN结构本身的一大弊端, 即不可并行计算, 这在数据量和模型体量逐步增大的未来, 是RNN发展的关键瓶颈。

实现过程

      选用学堂在线的数据集， 包括了39门课程的79186名学生的120542条注册活动日志，每门课程可能需要长达５周的时间。学习者行为记录信息有２个主要来源：浏览器和服务器，包括访问对象、讨论、导航课程、页面关闭、尝试解决问题、观看视频和浏览维基这７个事件。每个学生参加的课程的行为包括观看视频、尝试解决问题、参与课程模块等。另外，一名学生可以参加多门课程的学习。每个学生在每周的课程中都有一个标签，表明学生是否辍学或完成课程。

  实验中学堂在线数据集统计信息

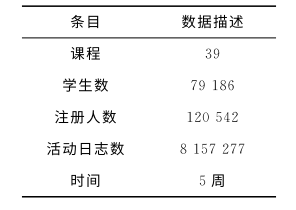
（1）数据提取

import pandas as pd
import matplotlib.pyplot as plt
import datetime
import torch
import torch.nn as nn
from torch.utils.data import Dataset, DataLoader
import math
from  sklearn.metrics import mean_squared_error
dataset=pd.read_csv(r"../dataset/pid167.csv")
dataset.head(5)

（2）数据预处理

X会作为后面GRU模型的输入，是一个4列n行的矩阵；X_Y矩阵y列是需要进行预测的目标。

def gru_X(series:pd.Series, n:int)->torch.Tensor:
    X=pd.DataFrame()
    X_Y=pd.DataFrame()
    for i in range(n):
        X['X%d' %i]=series.tolist()[i:-(n-i)]
    for i in range(n):
        X_Y['X%d' %i]=series.tolist()[i:-(n-i)]
    X_Y['y'] = series.tolist()[n:]
    X=torch.tensor(X.values).cuda()
    X_Y=torch.tensor(X_Y.values).cuda()
    return X,X_Y
X,X_Y=gru_X(dataset['167'],n)
X,X_Y

将数据分为X_train（训练输入）,X_test（测试输入）,Y_train（训练目标）,Y_test（测试目标），其中n等于gru_X的参数n，train_end是需要预测数据点个数（负数）。

def read_data(column:str,n:int,train_end:int)->pd.DataFrame:
    data_Y=dataset[column]
    data_Y=torch.tensor(data_Y.values).cuda()
    Y_train=data_Y[:train_end]
    Y_test=data_Y[train_end:]
    X,X_Y=gru_X(dataset['167'],n)
    X_train=X[:train_end]
    X_test=X[train_end:]
    return X_train,X_test,Y_train,Y_test
X_train,X_test,Y_train,Y_test= read_data('167', n,train_end)
X_train,X_test,Y_train,Y_test

（3）模型构建

class model_gru(nn.Module):
    def __init__(self,input_size:int):
        super(model_gru,self).__init__()
        self.gru=nn.GRU(
            input_size=input_size,
            hidden_size=4,
            num_layers=1,
            batch_first=False,
            )
        self.out=nn.Sequential(
            nn.Linear(4,1)
        )

    def forward(self,x:torch.Tensor):
        r_out,self.hidden=self.gru(x)
        out=self.out(r_out)
        return out

（4）模型训练

learning_rate = 1e-1
loss_list = []
for step in range(EPOCH):
    for tx, ty in loader:
        model=model.cuda()
        tx= tx.cuda()
        ty= ty.cuda()
        output = model(torch.unsqueeze(tx, dim=0))
        loss = loss_function(torch.squeeze(output), ty)
        optimizer.zero_grad()  # clear gradients for this training step
        loss.backward()  # back propagation, compute gradients
        optimizer.step()
    print(step, loss)
    if step % 10:
        torch.save(model, 'model.pkl')
torch.save(model, 'model.pkl')

（5）模型测试

Y=dataset['167']
test_index = len(Y) + train_end-n
train=[]
test=[]
for i in range(len(Y)-n):
    x = X[i:i+1]
    x = torch.unsqueeze(x,0)
    x=x.to(torch.float32)
    y = model(x)
    if i < test_index:
        train.append(torch.squeeze(y).detach() )
    else:
        test.append(torch.squeeze(y).detach())
    
train=torch.tensor(train).cuda()
test=torch.tensor(test).cuda()
train=train.data.cpu().numpy()
test=test.data.cpu().numpy()

（6）可视化

fig,ax=plt.subplots(1,1,sharex=True,figsize=(30,13.6),dpi=100)
ax.grid(color='gainsboro',linestyle='--',which='both',axis='both')
ax.plot(data_time[n:train_end], train, label='train')
ax.plot(data_time[train_end:], test, label='test')
ax.plot(data_time, dataset['167'], label='DATA')
ax.legend()
plt.show()

1.RNN模型大概的实现过程，以及应用方向。

2.GRU模型大概的实现过程，以及应用。

3.RNN模型与GRU模型的优缺点。

[1]刘儒君. 慕课学生辍学预测模型的研究[D].华中科技大学,2017.

[2]张聪. 基于特征工程的MOOC辍学预测研究[D].江西财经大学,2020.

[3]黄子亮. MOOC课程学生辍学行为预测方法研究[D].华南理工大学,2021.

[4]徐振国,张冠文,石林,安晶.MOOC学习者辍学行为的影响因素研究[J].现代教育技术,2017,27(09):100-106.

[5]陈立德. MOOC学习行为挖掘和辍学预测方法研究[D].西北农林科技大学,2018.

[6]Pardos Z A, Gowda S M, Baker R S J, et al. The sum is greater than the parts: ensembling models of student knowledge in educational software. ACM SIGKDD explorations newsletter, 2012, 13(2): 37-44.

[7]Hermans M, Schrauwen B. Training and analysing deep recurrent neural networks. Advances in Neural Information Processing Systems, 2013:190-198.