利用贝叶斯网络对pisa数据进行分析

1. 实验目的：

本实验旨在运用贝叶斯网络对pisa（国际学生评估项目）数据进行深入分析。贝叶斯网络是一种强大的概率图模型，能够有效地表达和处理变量之间的不确定性关系。通过此分析，我们旨在实现以下几个具体目标：

• 揭示变量间的依赖关系：贝叶斯网络的核心优势在于其能够揭示数据中变量间的依赖性和条件独立性。通过构建贝叶斯网络模型，我们希望识别出影响学生学业表现的关键因素，以及这些因素之间的相互作用。

• 预测和推断：利用构建的贝叶斯网络模型，我们可以对学生的学习成绩进行预测，并在给定某些变量值的情况下推断其他变量的可能值。这对于理解学生表现背后的驱动因素及其影响程度至关重要。

• 决策支持和政策制定：通过分析pisa数据集中变量的概率关系，该实验旨在为教育决策者和政策制定者提供有价值的见解。这些见解可以用于优化教育资源配置、制定针对性的教学策略，以及改进学生评估方法。

• 验证现有教育理论：该实验还旨在使用实证数据检验现有的教育理论。通过分析不同国家和地区的学生数据，可以验证或质疑某些教育理论的普适性和有效性。

• 促进教育公平：通过识别影响学生学习成绩的关键因素，该实验有助于发现可能导致教育不公平的因素，为制定更公平的教育政策提供数据支持。

2. 实验工具：

spssmodeler 软件

3. 实验原理：

贝叶斯网络（bayesiannetwork），又称信念网络（beliefnetwork）或是有向无环图模型（directedacyclic graphicalmodel），是一种概率图型模型。从形式上说，贝叶斯网络是由一组以单向箭头相连的节点以及与每个节点相对应的概率函数所构成的网络。

贝叶斯网络是一种不定性因果关联模型，是将多元知识图解可视化的一种概率知识表达与推理模型，更为贴切地蕴含了网络结点变量之间的因果关系及条件相关关系，且具有强大的不确定性问题处理能力，能有效地进行多源信息表达与融合。

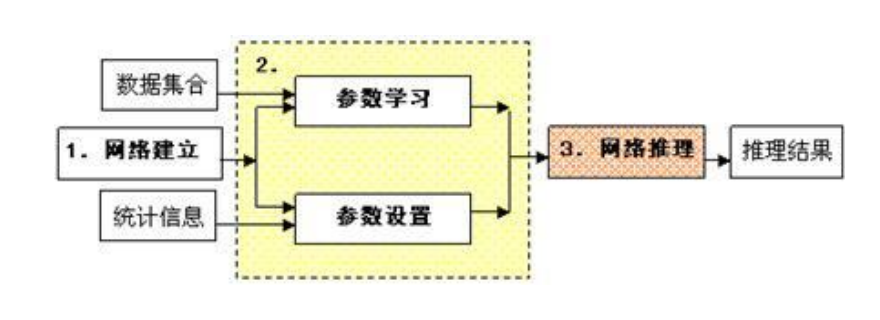
贝叶斯网络根据每个节点的概率表，在给定部分（一个或多个）节点状态值的前提下，对其余全部或部分节点的概率分布进行预测的过程即为网络的推理过程。贝叶斯网络的分析流程通常由三个步骤组成，即网络建立，参数学习或参数设置，网络推理。

4. 实验步骤：

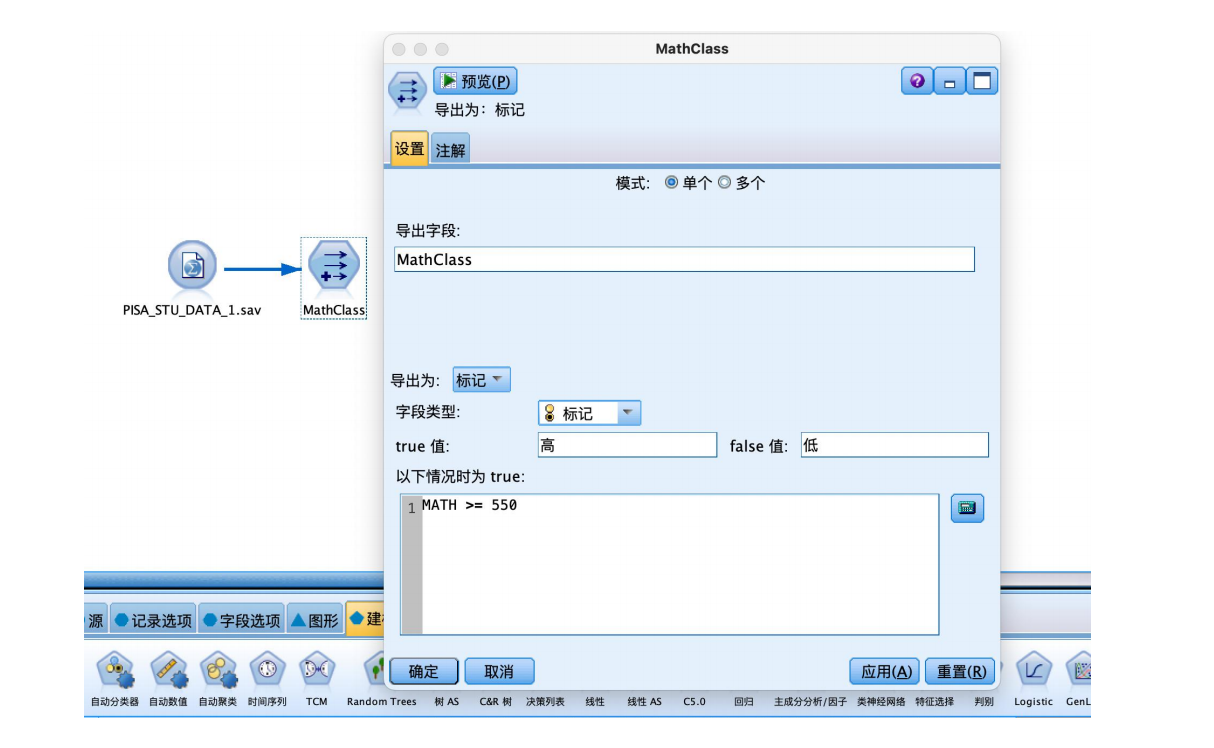
① 从“源”中拖拽出“statistics文件”到数据流编辑区，并编辑数据，从“字段选项”选项卡中拖拽“导出”节点到数据流编辑区，建立连接，建立好如图数据流，并编辑“导出”节点，在导出字段框中输入mathclass，选择导出为标记，在true值框中输入“高”，false值框中输入“低”，并点击公式编辑器按钮，在弹出的表达式构建器中输入“math>=550”。

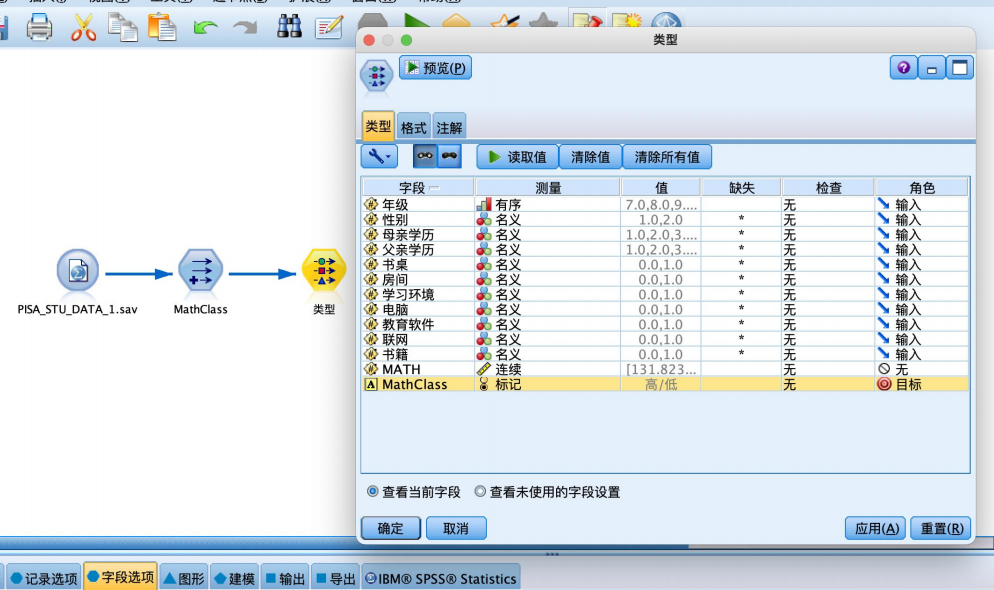
②选择“字段选项”选项卡，拖拽“类型”节点到数据流编辑区。将“类型”节点与“导出”节点建立连接，右键并对其进行编辑，将十次数学成绩以及“math”字段的角色设置为“无”，“mathclass”字段的角色设置为“目标”，其余字段设置为“输入”。

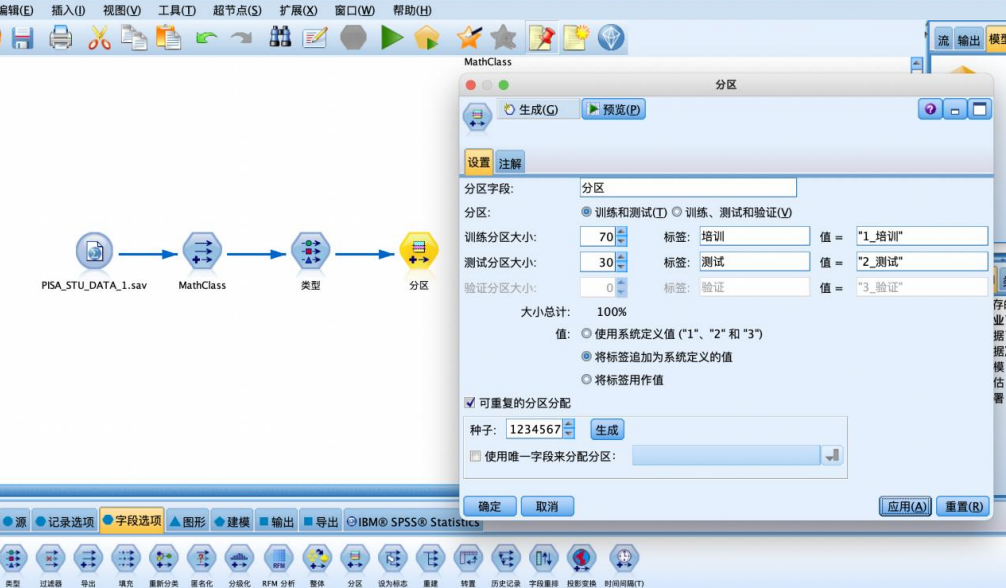
③ 从“字段选项”选项卡中拖拽“分区”节点到数据流编辑区，与

“类型”节点连接，并右键编辑参数，设置70%的数据用作训练，

30%的数据用作预测。

④建立如图所示数据流，从“建模”选项卡拖拽“贝叶斯网络”节点到数据流编辑区，与“分区”节点建立连接，并进行属性的设置，选中“使用分区数据”“tan”“包括功能选择预处理步骤”“最大似然法”，并设置“贝叶斯网络”节点的“专家”属性，专家选项卡用于设置模型析的其他参数。

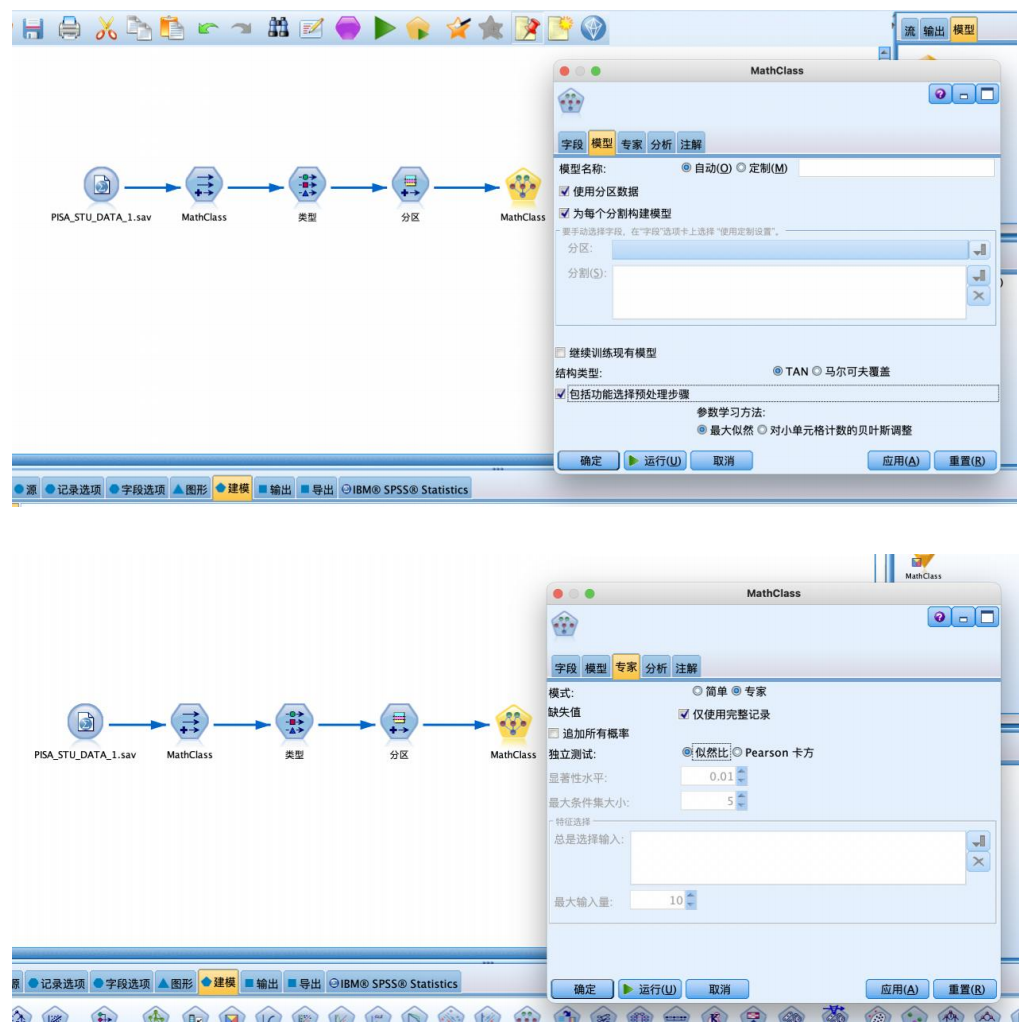
⑤ 运行即可得到结果。

5. 实验结果：

在模型中，给出了贝叶斯网络和预测变量的重要性两张图表。

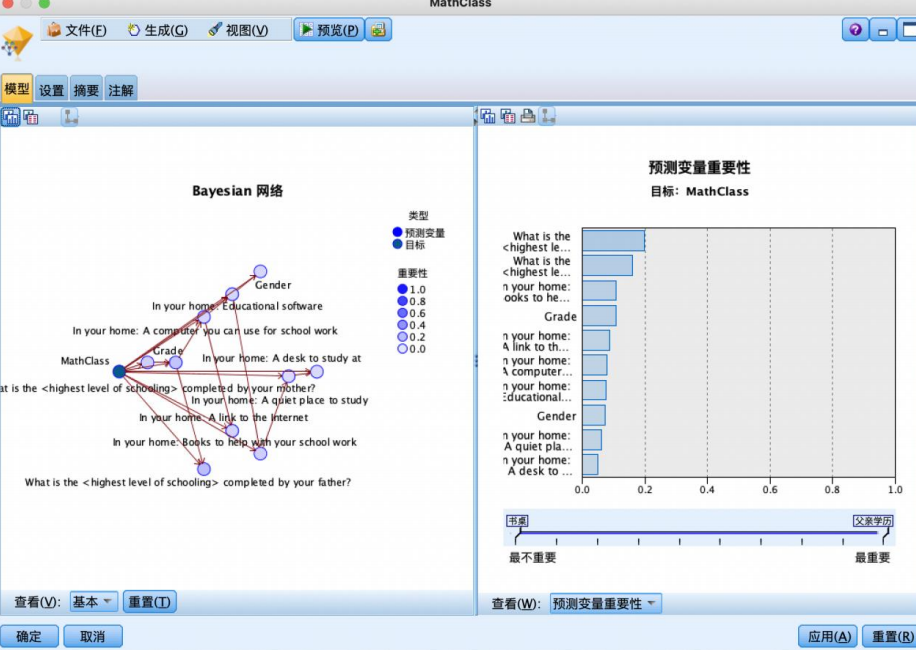
左侧显示的是 tan贝叶斯网络。深色节点代表目标变量，是其余各节点的父节点。浅色节点代表输入变量。输入变量的重要程度仍以深浅表示，颜色越深则重要程度越高。同时，变量重要性的排序结果也默认以图形方式显示在窗口的右侧。输入变量重要性的测度指标是输入目标变量独立性检验的1-概率p值经归一化处理后的结果。

本例中，影响学生数学成绩的最重要因素是父亲最高学历，其次是母亲最高学历、书籍、年级、联网、电脑、教育软件、性别、学习环境、书桌等。

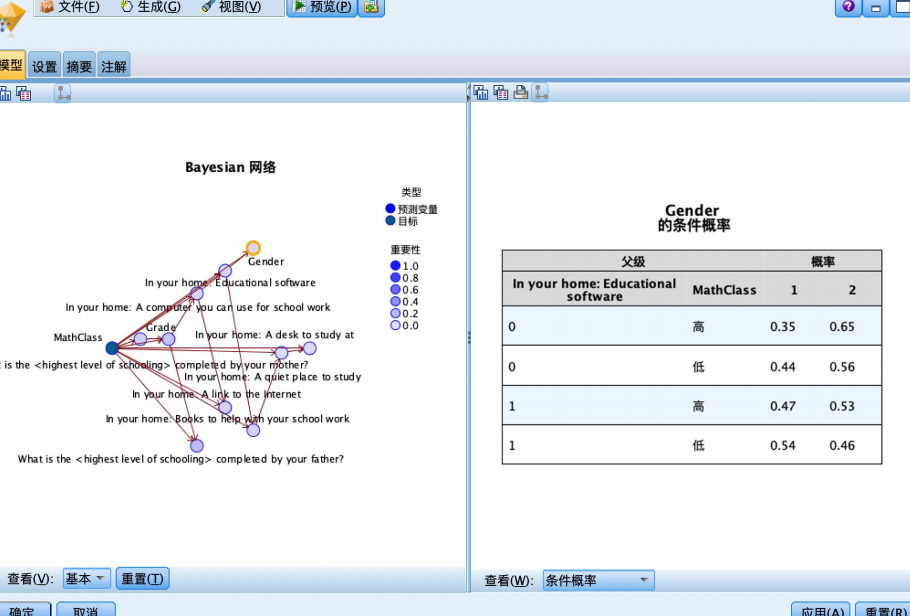
选择左侧窗口中的某个节点，可浏览相应节点的参数结合，如图显示了gender节点（1是女，2是男）的参数几何。该节点有两个父节点即mathclass和教育软件，参数是给定父节点下的条件概率参数集合。教育软件包括2个水平，分为2个组，性别有2个水平，分为2个组。可见，家中没有教育软件且成绩较高的学生中，女生概率最高，为0.65。

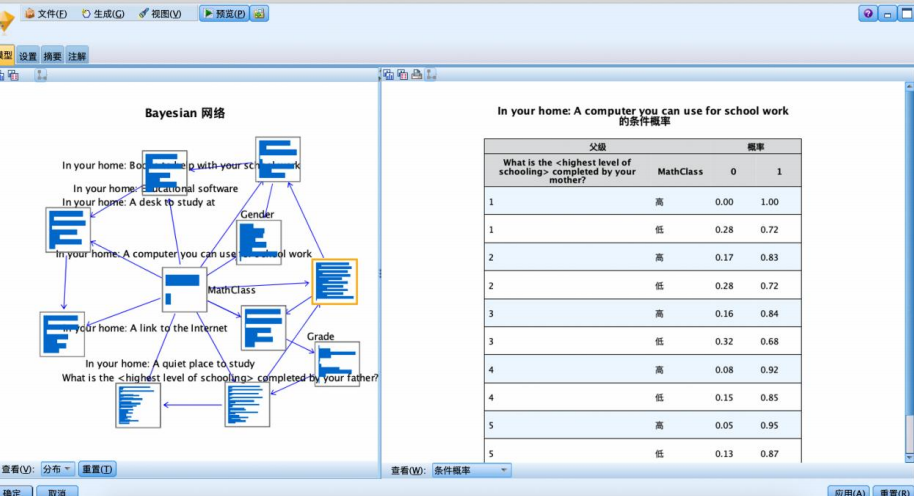
选择左侧窗口“查看”下拉框中的“分布”选项，网络节点将显示为条形图。每个输入变量节点的条形图分为两组显示，分布对应目标变量的两个类别。例如下图，展示了做家庭作业时可用的电脑变量的参数集合。

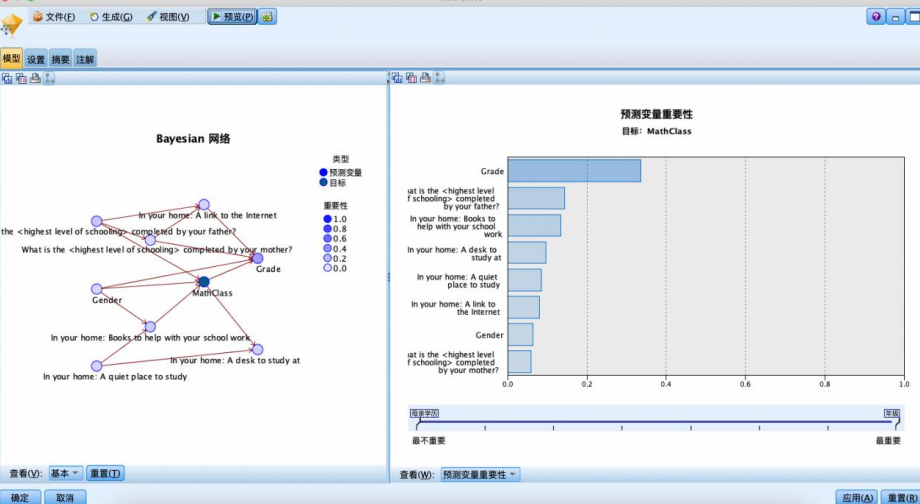
回到“模型”选项卡，选择“马尔科夫覆盖”选项，其他不变，点击运行，再次查看结果。

此时得出的结论为，影响学生数学成绩的最重要因素是性别，其次是父亲最高学历、书籍、书桌、学习环境、联网、性别、母亲最高学历等。

6. 分析与讨论：

1. 实验分析

• 变量间的依赖关系：贝叶斯网络通过揭示了数学成绩（mathclass）与其他因素之间的依赖关系。例如，父母的最高学历、书籍的数量、年级、联网情况、电脑使用、性别等因素均与学生的数学成绩有关联。这表明教育成果受多种因素的共同影响。

• 重要性分析：实验结果显示，父亲的最高学历是影响学生数学成绩的最重要因素，其次是母亲的最高学历和家庭的资源状况（如书籍的数量、电脑使用等）。这强调了家庭背景和资源对学生学术成就的重要性。

• 性别差异：性别作为一个重要变量出现在影响学生数学成绩的因素中，这可能反映了性别在教育成果上的差异，需要进一步探究其背后的原因和机制。

• 马尔科夫覆盖的结果差异：使用马尔科夫覆盖作为模型处理方式后，结果显示性别成为了影响学生数学成绩的最重要因素。这表明不同的模型处理方式可能导致结论上的显著差异，强调了模型选择对于数据分析结果的影响。

2. 讨论

• 家庭背景的影响：家庭背景，特别是父母的教育水平，对学生的学术成就有显著影响。这可能与家庭教育资源和父母对子女教育的重视程度有关。

• 资源的重要性：家庭的物质资源，如电脑和书籍，也是重要因素，这强调了优质教育资源对提高学生学业成绩的重要性。

• 性别差异的考量：性别因素的显著性提示我们，教育过程中需要关注性别差异，探索不同性别学生的特定需求和教育策。

• 模型选择的重要性：不同的模型处理方法可能导致结论的差异，这强调了在进行数据分析时模型选择的重要性。马尔科夫覆盖与传统贝叶斯网络方法得出的主要影响因素不同，表明对同一数据集的不同处理可能揭示不同的信息。

• 教育政策的启示：本实验结果可为教育政策制定提供依据。例如，强调家庭教育资源的重要性，促进性别平等的教育环境，以及为不同家庭背景的学生提供更多支持。

• 未来研究方向：未来研究可以进一步探究家庭背景和资源对学生学业成绩的具体影响机制，以及性别差异背后的原因。此外，也可以考虑使用更多变量和更复杂的模型来提高分析的准确性和深度。

7. 总结或个人反思

1. 实验总结

本实验通过贝叶斯网络对pisa数据集进行了深入的分析，揭示了学生数学成绩与各种因素之间的复杂关系。

实验结果表明，学生的数学成绩受到多种因素的影响，其中家庭背景（特别是父母的教育水平）、家庭资源（如书籍和电脑的使用）以及性别都是重要的影响因素。这些发现不仅丰富了我们对教育成果影响因素的理解，而且对教育政策制定和学校教育实践提供了有价值的指导。

2. 个人反思

• 数据处理的重要性：本实验体现了数据预处理和模型选择在数据分析中的重要性。正确的数据处理和恰当的模型选择对于获得可靠和有意义的结果至关重要。

• 统计学习的价值：贝叶斯网络作为一种复杂的统计学习方法，其在教育数据分析中的应用显示了统计学习工具在解决实际问题中的强大能力。这增强了我对统计学习方法实用性的认识。

• 多角度思考：实验结果表明，影响学生学业成绩的因素是多方面的。这提醒我在面对复杂问题时，需要从多个角度进行思考，避免简化或偏颇的理解。

• 教育公平的关注：家庭背景和资源的重要性强调了教育公平的问题。作为一个教育研究者，这促使我更加关注教育公平问题，并思考如何通过教育政策和实践来缩小不同群体间的教育差距。

• 未来的研究方向：本实验开拓了我对未来研究方向的思考。例如，进一步探究性别差异背后的原因，或者研究特定家庭背景对学生学业成绩的具体影响。

本次实验不仅增强了我对贝叶斯网络及其在教育数据分析中应用的理解，也促使我对教育问题有了更深入的思考，特别是关于教育公平和多元影响因素的认识。这些认识和思考将对我未来的研究和实践产生深远的影响。