-
协同学习任务6:学习迁移及为迁移而教(第九章 part 2)
普通类 -
- 支持
- 批判
- 提问
- 解释
- 补充
- 删除
-
-
章节导学
-
第一部分 学习迁移概述
(一)迁移的定义
学习迁移是“在一种情境中的技能、知识和理解的获得或态度的形成,对另一种情境中的技能、知识和理解的获得或态度的影响”。简单地说,学习迁移是一种学习对于另一种学习的影响。
(二)迁移的分类

-
第二部分 早期迁移理论
1.形式训练说(古希腊罗马)
2.相同元素说(桑代克、伍德沃斯)
3.概括化理论(贾德)
4.三维迁移模型(奥斯古德)
具体内容见拓展资源:早期迁移理论
活动1:讨论交流 题海战术与迁移
题海战术是指在面对考试时进行大量练习,通过对知识点和题目类型的不断重复,达到巩固知识点的目的。请大家在下方活动中完成讨论:
•题海战术以哪一种早期迁移理论作为基础?
•题海战术在迁移方面有哪些优缺点?适合或不适合用于哪种类型知识的学习?
请个人(小组)交流讨论完成以上问题,在下面讨论交流区阐述观点。
-
活动1 题海战术与迁移
-
第三部分 为迁移而教
教学建议:
①整合学科内容,注重各门学科的横向联系。
②加强知识联系,重视简单知识技能与复杂知识技能、新旧知识技能之间的联系。
③强调概括总结,培养和提高学生的概括总结能力,讲解原理原则时多举例,结合具体情境使学生掌握实质。
④重视学习策略,有意识地帮助学生在学习时掌握概括化的认知策略和元认知策略。
⑤培养迁移意识,通过反馈和归因控制等方式形成学生对学习和学校的积极态度,结合学生的年龄特点创设学校和学习气氛,帮助学生在学习前形成良好的心理准备状态
-
案例分析 为迁移而教
【案例1】在学习二元一次方程时,教师一般以一元一次方程进行导入


【案例2】王老师在讲解《岩石的组成》一课教学中,为了组织好学生在课堂上的探究活动,师生共同准备好用于观察和实验的各种材料。除教师准备好教学中所需的实验材料,如石英、长石、云母、花岗岩、石墨、硫磺、石膏、石岩等外,还指导学生自己收集并准备一些易于获得的材料,如石块、砖块、玻璃、木块、塑料等。教学时一是有顺序地引导学生分组观察,提示他们用手摸、捏后寻找矿石外表的相同点;二是提示学生注意观察实验现象,以便于告诉老师“看到了什么,通过体验和观察,知道了什么?”;三是精心组织研讨,引导学生思维,逐步培养学生总结概括能力。
【案例3】在英语 Unit1 Food for thought,单元教学中,单元语境是“人与社会”、“人与自我”。以食物为主题,介绍了健康的生活方式和不同国家的饮食习俗,重点是不同文化之间的交流、沟通和包容。文章语篇类型为记叙文,以第一人称讲述了中英混血男孩家庭爸爸、妈妈和自己不同的饮食偏好及每个家庭成员面对文化冲击的不同观点。
在教学活动设计时,教师设计了角色扮演活动,使学习者在角色扮演中内化本课所学文化意识,分析评价他人表现,并在活动中迁移创新,体会多样的文化。
活动2 讨论交流 为迁移而教
为什么教学时要考虑迁移?如何理解“为迁移而教”?为了实现为迁移而教,案例中的教师的教学设计运用了哪些促进迁移的教学策略?
请个人(小组)交流讨论完成以上问题,在下面讨论交流区阐述观点。
-
活动2 为迁移而教
-
案例拓展
案例1:求图形面积
迁移受理解性学习的程度的影响,而非仅靠记忆事实或墨守成规。
•理解法
理解法鼓励学生去了解平行四边形的结构关系。例如,通过把一个三角形从一边移到另一边,平行四边形可以重新组合成长长方形。由于学生知道如何求长方形的面积,一旦他们发现适合的结构关系,求平行四边形的面积便变得轻而易举。
•死记法
所谓死记法就是教学生划一条垂直的辅助线,然后让学生应用所记的解决问题公式。
•迁移
两组学生在解决平行四边形面积这样的典型问题时,表现都十分出色。然而只有采用理解法的那一组能够把知识迁移到新问题上,如图 3 图形的面积。
或区分出能解决和不能解决的问题,如采用死记法的那一组对新问题所做的反应是“我们还没有学过”。
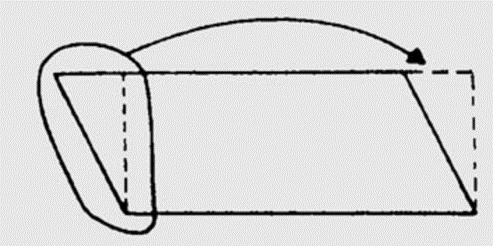
图1 理解法 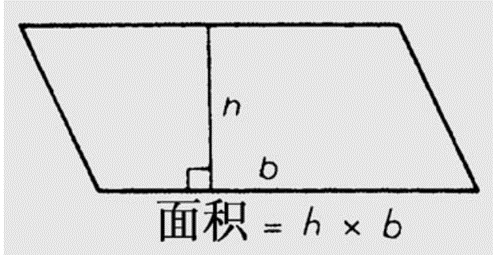
图2 死记法 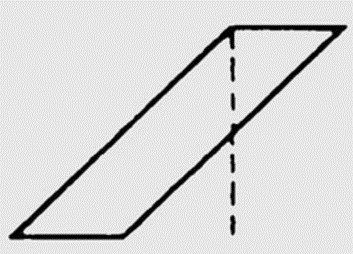
图3 迁移1 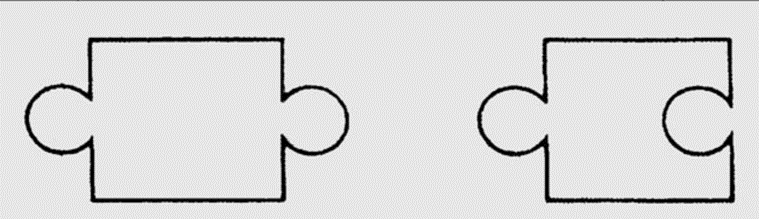
图4 迁移2 -
案例拓展
案例2 明确的学习任务为迁移学习做准备
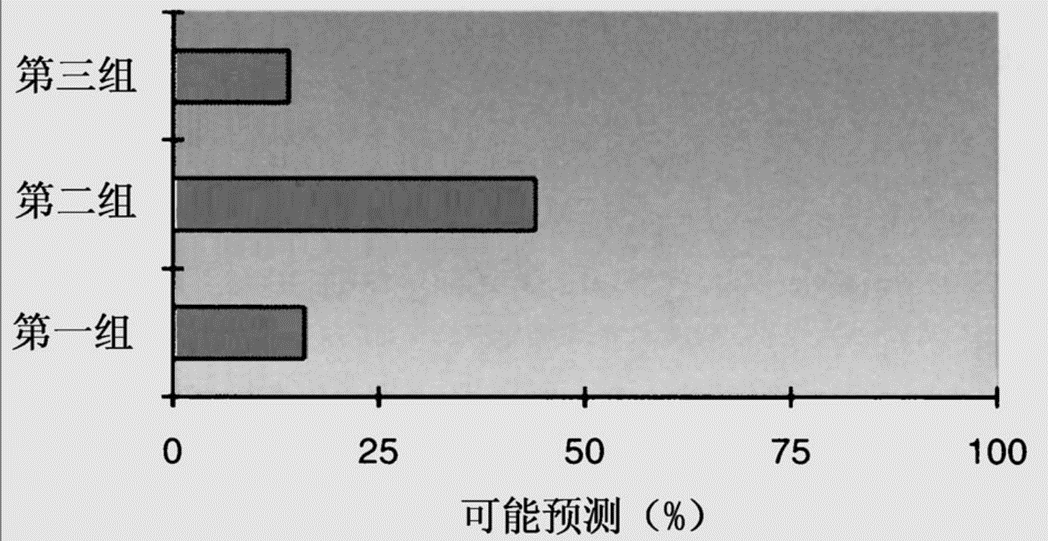
三个组别的大学生接受不同类型的图式理论和记忆的指导,然后完成一项迁移任务。该任务要求他们对一项新的记忆研究结果作详细的预测。
第1组学生阅读并概述了一篇以图式理论为主题的课文,然后听一个为他们设计的讲座,该讲座的目的是要帮助学生组织知识,进行理解性学习。
第2组没有阅读课文,而是主动地比较源自记忆图式实验的简化数据组,然后听与第1组相同的讲座。
第3组没有听讲座,而是花两倍于第2组的时间处理数据。
在迁移测试中,第2组的学生比第1组和第3组的学生表现得更好。他们对数据的处理为其听讲座奠定了基础。讲座是必不可少的,第3组的糟糕表现说明了这一点。
学习者(尤其是学校环境中的学习者)常常会遇到没有明确意义和清晰逻辑的任务。对他们来说,一开始便要从事理解性学习是有困难的。他们也许需要时间去探究基本概念,生成与其他已有信息的联系。一下子接触大量主题会妨碍学习和随后的迁移,因为学生(a)只是学习孤立的,没有经过组织和联系的事实,或(b)接受他们无法掌握的组织原则,因为他们缺乏足够的具体信息使这些原则变得有意义。为学生提供先摸索与主题相关的具体信息的机会,是要创立一个“讲授时机”,使他们从有组织的讲授中(通过随后的迁移能力测定)学到的东西要比最初没有这些具体机会的学生要多。
-
有问题请提问
-
学习活动评分标准
-
-
- 标签:
-
加入的知识群:

.jpg)

学习元评论 (0条)
聪明如你,不妨在这 发表你的看法与心得 ~