-
知识点追踪模型
普通类 -
- 支持
- 批判
- 提问
- 解释
- 补充
- 删除
-
-
学习目标
知识追踪的本质是根据学生的历史学习记录来推测任意时刻学生对于知识点的掌握程度,进而预测学生的未来成绩。通过本章的学习,学习者应达到以下目标:
1.了解知识点预测模型的的基本概念和研究进展;
2.掌握知识点追踪模型的基本原理;
3.能够利用BTK模型和DKT模型实现知识点追踪。
-
学习建议
1.学习的建议时长为6课时;
2.阅读相关文献或书籍。
-
思维导图
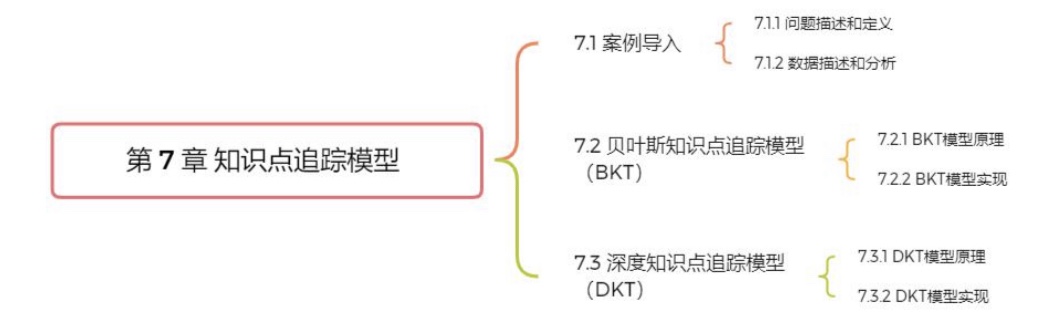
-
7.1案例导入
7.1.1问题描述和定义
一、教学评价过程中出现的问题
在上学的时候经常碰到过这样的状况,老师会经常考试,那么老师不能平白无故的给你考试,为什么要考试呢?
考试的主要目的就是为了衡量学生对于某一知识的掌握水平,最初,教育测评还没有依赖智能教育的时候,对学生进行测评主要是通过【经典测验模型(Classical Test Theory, CTT)】,简单来说,就是给学生们统一出了一份卷子,固定好每道题的分值,然后单纯的通过学生对这一份卷子的答题结果进行评价,学生得多少分就代表他的能力。同样,卷子难度的评价也是通过学生对这道题的答题情况分布来进行的。但是,这显而非常不够客观,如何能够更快更精确的评价学生的能力呢?
二、何为知识追踪模型?如何帮助教学?
1、何为知识追踪模型?
知识追踪模型是模拟学习者知识掌握情况的一个典型模型,由Atkinson 于1972 年首次提出,每个知识点由猜测率、学习率、失误率和学习知识之前的先验概率4 个参数组成(Pardos & Heffernan,2010),并由Crbett 和Anderson (1994) 引入智能教育领域,目前已经发展成为智能辅导系统中对学习者知识掌握情况建模的主流方法。
实际上知识追踪是一种特殊的隐马尔科夫模型(hidden markov model, HMM),每一个节点都通过条件概率表(conditional probability table,CPT) 来量化父节点对自身的影响

2、知识追踪模型运用于教学评价典型案例
某研究选取了重庆市某小学六年级四个班的213名学生为研究对象,通过利用贝叶斯知识追踪模型这一典型的学生知识评估方法,对研究对象作答数据进行了训练和分析,得到了其对于不同知识点的掌握程度及数学能力水平,并且最终形成了个性化认知诊断报告,帮助教师更好的了解学生知识水平,调整教学策略,从而提升教学效率。
7.1.1数据描述和分析
一、数据描述
1、实验对象
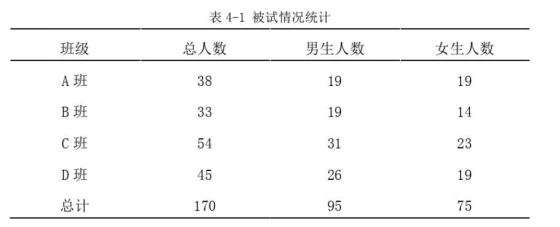
该研究的实验对象为重庆市某小学六年级四个班的学生,共213名,最终收到的有效测验结果为170份。其中班级A人数为38人,班级B人数为33人,班级C人数为54人,班级D人数为45人,具体的分布情况如表所示。
2、测验试题设计
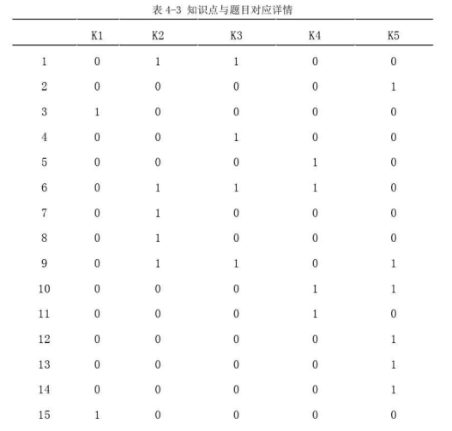
通过与学校相关老师进行沟通之后,综合测验时长、学习进度等多种因素,本次试题最终将测试内容确定为六年级上学期的5个内容域,包括分数的概念(k1)、分数的加法(k2)、分数的减法(k3)、分数的乘法(k4)和分数的除法(k5),具体有关内容域的描述如表所示。

本次测验由教师提供的32道选择题组成,涵盖了上述5个内容域。题目作答情况由二进制结果“1”和“0”来表示。“1”表示学生作答正确,“0”表示学生作答错误。表4-3展示了知识点和试题的对应情况,并且我们可以看出,存在同一题目包含多个知识点的现象。由于在实际测验中,往往一道题目涵盖多个知识点,仅根据答题正确与否无法准确的判断学生知识掌握情况,因此需要使用知识追踪模型来对学生知识水平进行追踪和判断。
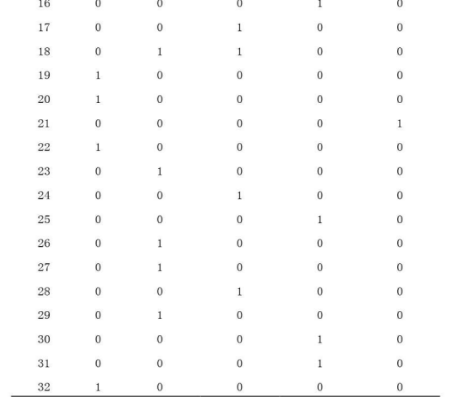
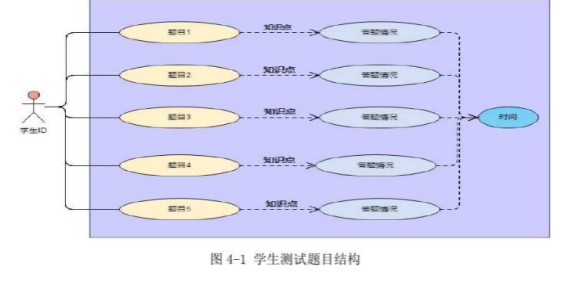
测试结果包含学生的学号、答题情况、知识点对应情况、题目所花费时间等信息,具体的结构如图所示。
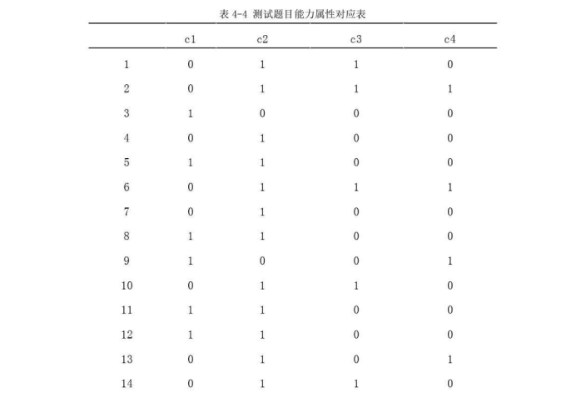
该研究将小学生数学能力分为以下四种:概括能力(c1)、运算能力(c2)、思维能力(c3)和解决问题能力(c4)。
概括能力是指学生能够将数学材料中的语言进行总结和概括,将其转化为具体的数学问题的能力。运算能力是指学生能够运用数学符号和公式对数字进行准确计算的能力。思维能力则是指学生能够通过思考摒除冗余信息并选择合适方式的能力。解决问题能力则是指学生能够利用已有的数学知识,创造性的解决现实生活中问题的能力。测验中题目所考核的能力如表所示。

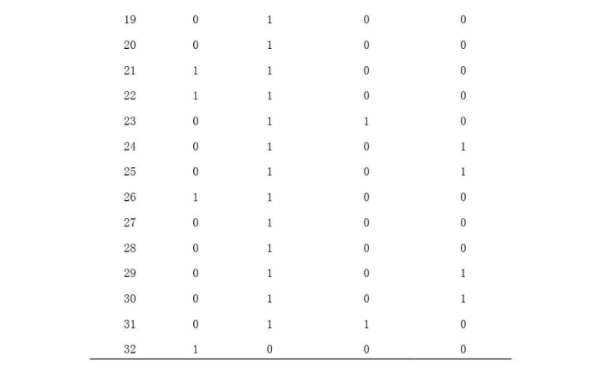
3、数据处理具体流程
该研究使用了在标准贝叶斯知识追踪模型基础上增加了知识点关系参数矩阵的CS-BKT模型对数据进行训练和分析,具体流程如图:
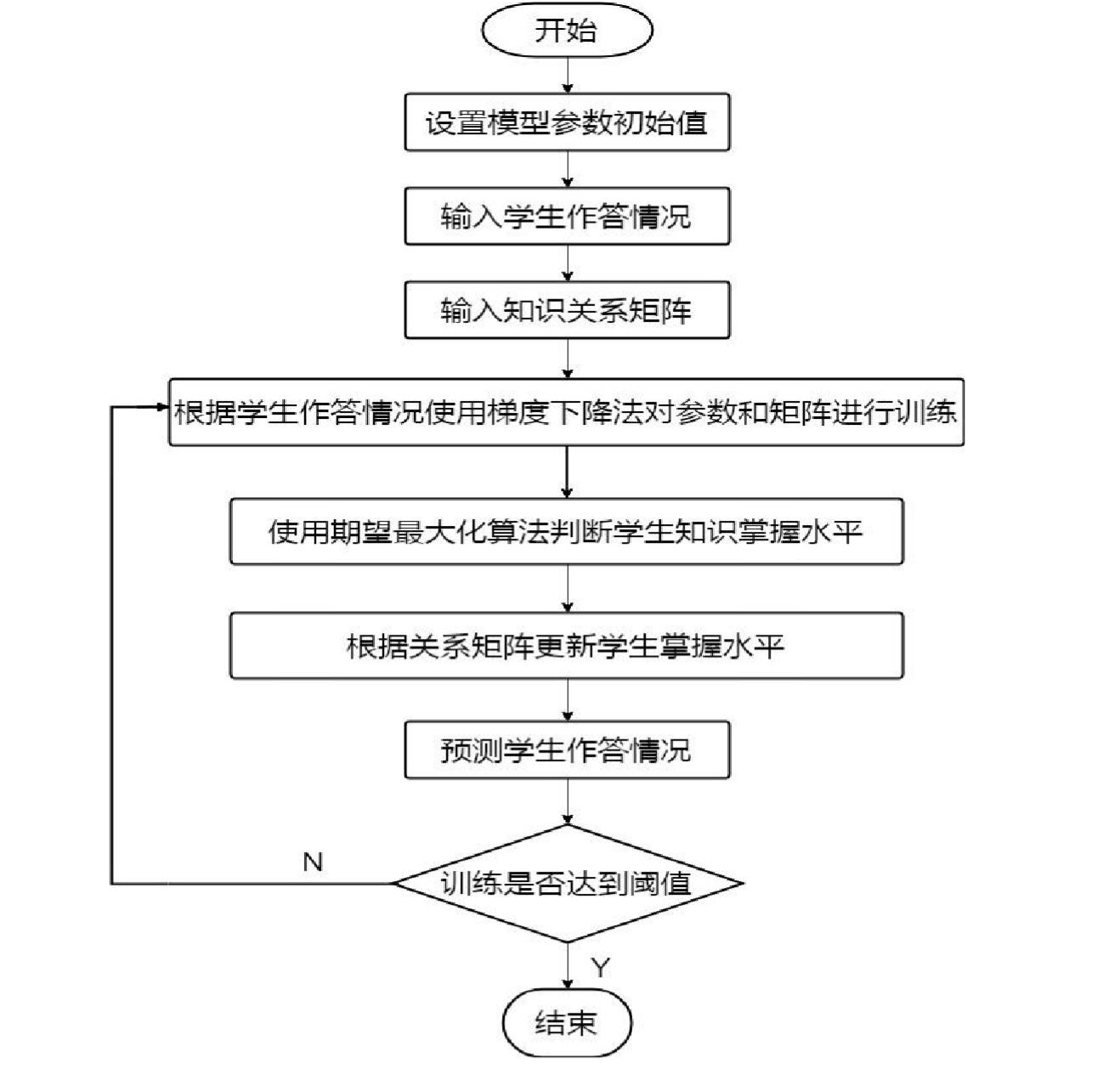
该流程可以概括为以下步骤:
(1)首先根据知识技能数量来设置初始参数值
(2)输入不同学习者的作答情况
(3)输入初始知识技能之间的影响关系矩阵
(4)根据学生答题情况使用梯度下降方法对参数和知识矩阵进行训练和更新
(5)使用期望最大化算法计算学生技能水平
(6)利用更新后知识之间关系矩阵值对技能水平在第5步的基础上重新进行计算
(7)预测学生下一道题目答题情况
(8) 重复第4到7步,直到达到阈值根据学生作答数据,使用知识追踪模型对学生数学能力进行计算,得出学生整体数学能力情况,如表4-9 所示。由表4-9 可以看出,运算能力平均值最高,说明学生的运算能力在四种能力中掌握情况最好。概括能力标准差最小,说明学生掌握概括能力的差异较小。思维能力的平均值最低,标准差最大,可以认为思维能力是一种较高要求的数学能力,需要学生重点训练和提高。解决问题能力的标准差也较大,教师应重点关注该能力较差的学生,从而进行个性化辅导。
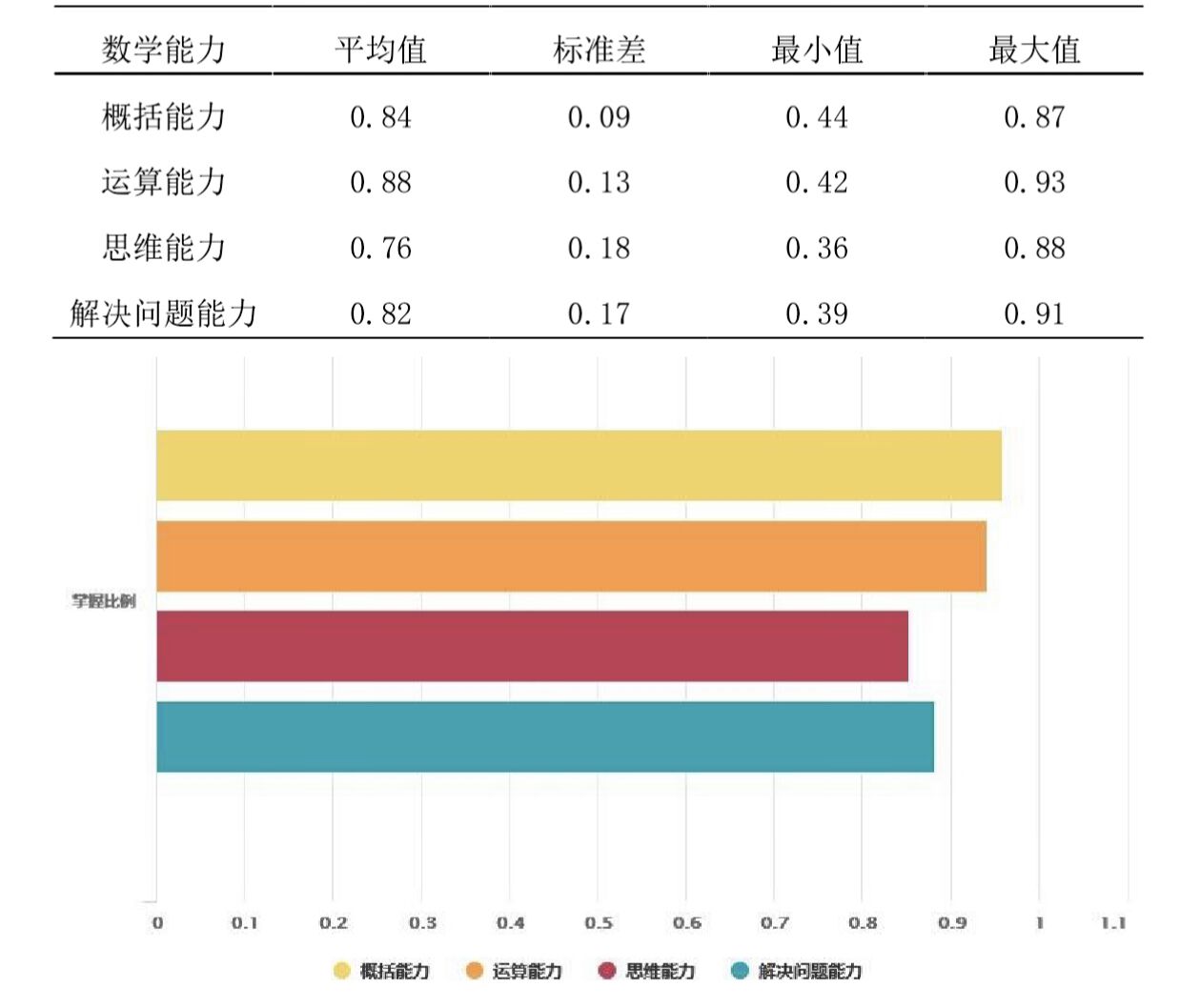
图展示了学生掌握不同数学能力的比例,由此可以看出,概括能力的掌握人数最多,而思维能力的掌握人数最少,因此,教师在日常教学中应该加强学生思维能力的锻炼.
-
7.2 贝叶斯知识点追踪模型(BTK)
贝叶斯模型在数据分析中一般用来解决先验概率、分类实时预测和推荐系统等问题,为了理解一下贝叶斯的概念,我们先来看一个例子:
如果大家了解过概率论统计学的,应该可以看出来,上面的两个问题分别需要用先验概率和后验概率进行解答。所以,我们先来了解一下先验与后验的概念。
7.2.1 先验与后验
我们直接举个例子来说明: 今天早上我喝了一杯凉水,那么中午我会不会拉肚子? 这里可以看出“拉肚子”是一种事实结果,而造成拉肚子的影响因素假设只有喝凉水,那么这个问题实际上是要求出在“喝凉水”条件下“拉肚子”的概率,也就是求: P(拉肚子|喝凉水)——先验事件当中的条件概率 通俗点说,先验事件就是由因求果,先验概率也就是根据以往经验和分析得到的概率,最典型的代表就是抛硬币,抛一个硬币求其正面的概率,就是已经知道了“硬币正反面概率都是0.5”的条件,求出“硬币是正面”的“结果”的概率。 而后验事件则是由果求因,也就是依据得到"结果"信息所计算出的最有可能是哪种事件引起的,用上面这个例子就是: 中午我拉了肚子,那么我早上喝了一杯凉水的概率是多大? 换言之,“拉肚子”是结果,我在已经知道结果的前提下,求“喝凉水”的原因的概率,也就是: P(喝凉水|拉肚子)——后验概率 而先验与后验的基础都是条件概率,其公式是:
P(A|B)=P(B|A)*P(A)/P(B)
也就是:“拉肚子”时“喝凉水”的原因的概率=“喝凉水”时“拉肚子”的概率*“拉肚子”的概率/“喝凉水”的概率。
7.2.2 BTK模型原理
贝叶斯知识追踪模型(Bayesian Knowledge Tracing Model,BKT)由Corbett, A. T. 和 Anderson, J. R.在1995年提出 ,并将其引入现代化 ITS(intelligent tutoring system),通过动态贝叶斯网络模拟学生的知识水平,对学生知识状态进行建模,建立知识状态之间的动态转换。随后,许多学者对BKT模型进行了扩展,使其更加个性化。BKT模型其实质就是一个标准的隐马尔可夫模型(hidden Markov model,HMM),它基于一阶隐马尔可夫过程构建。其中,“隐含状态”为学习者内隐知识状态,“外显状态”为学习者作答表现。BKT模型包含多个参数,可以通过最大期望(Expectation–Maximization,EM)算法进行估计得 到。BKT模型的工作机制如图7.2.1 所示,当学习者完成题目的作答后,BKT 模型便依据其作答正误,结合失误或猜对概率,利用贝叶斯公式对其此时的知识掌握状态进行直接估计。此外,BKT模型还可以基于已有数据,预测学习者在具有相同知识点但尚未作答的题目上做对的概率。
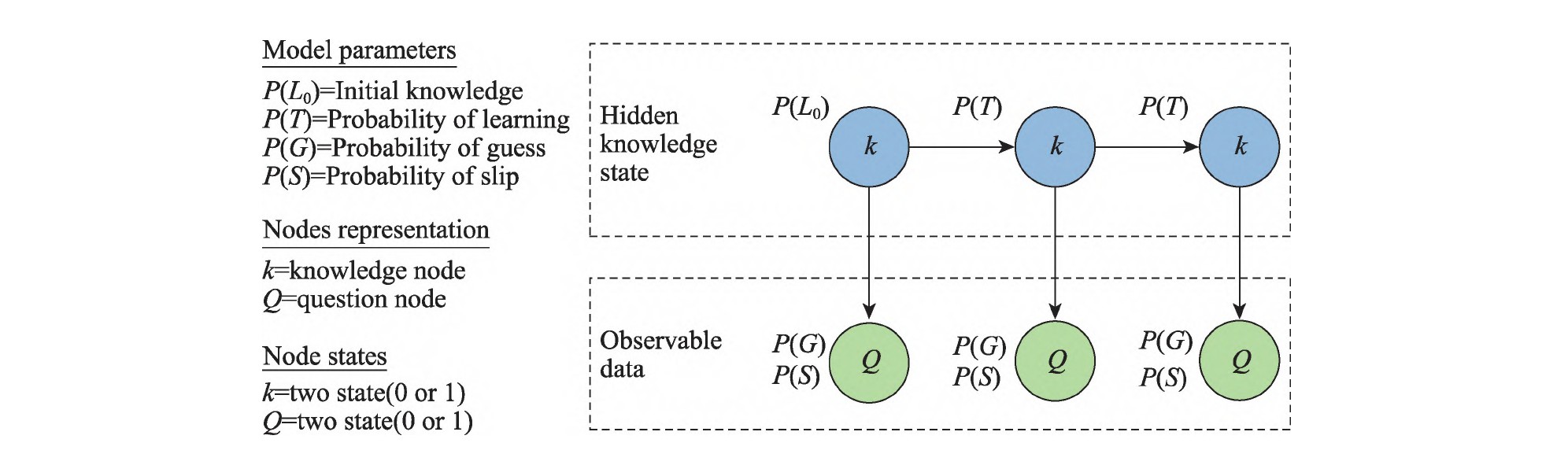
图7.2.1 BTK模型结构
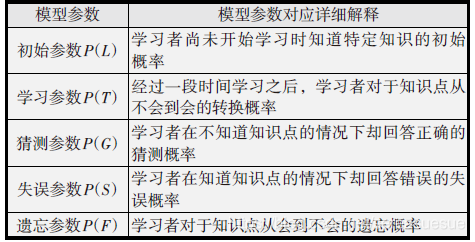
BTK将学生所需要学习的知识体系划分为若干个知识点。而学生的知识状况则被表示为一组二元变量,每个二元变量表示其中一个知识点是否被掌握,即学生处于“知道这个知识点”和“不知道这个知识点”两种状态之一。这是一种将学生的知识状态作为一套隐含变量的表示方式,通过学生回答问题 的正确与否来更 新隐含变量的概率分布。也就是说,观测变量同样也是二元的。 具体来说,BTK假设对于知识存在4个参数, 如表1所示。表中,p(L0)和p(T)是知识参 数,主要用于表示学生的学习状态。p(L0)指的是学生在尚未接触该学习系统时,某个知识点就已经被其掌握的概率;p(T)指的是学习效率,即经过了一 些学习机会之后,对于该知识点从不懂到懂的转换概率。另外,BTK假设学生不会遗忘,也就是说,对于一个知识点从懂到不懂的转换概率为0。 而 p(G)和p(S)作为用户的表现参数。p(G)是猜对的概率,即学生即使不知道某个知识点仍然正确回答的概率;p(S)是 犯错的概率,即学生知道该知识点,但是仍然 不小心回答错误的概率。当 p(G)和 p(S)为0时,学生回答问题的结果将会100%反 映 学生掌握该知识点的 情 况;而当 p(G)和 p(S)为 0.5时,学生回答问题的结果所反映的知识状况具有最大的不确定性。
表1 BTK的四个参数

不同的知识点在难度和所需要的练习上有很大的差别,所以各个知识点需要分别训练这样的一组参数。
根据以上对参数的定义,很容易得到以下几个公式。
1)学生答对题目的概率被解释为在知道知识点的情况下没有犯错,以及在不知道知识点的情况下猜对的概率之和,即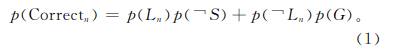
2)学生不会遗忘,而按照p(T)的学习效率加强 对知识点的理解,即

3)在训练好参数之后,根据数据对知识状况进行推断。
当答对题目时:
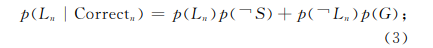
答错题目时:
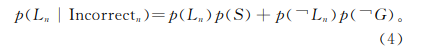
不难看出,贝叶斯知识跟踪模型其实就是 一 种特殊的隐马尔科夫模型 (hidden markov model,HMM)。用户在学习过程中的学习状态是随着时间变化的。
从 HMM 的角度来看,相应的参数如表2至表4 表示。

7.2.3 BTK模型的应用
贝叶斯知识追踪模型自提出以来,便被广泛的应用于教育领域。主要可以分为智能教育辅助系统、在线视频课程和认知诊断三个方面。
(1)智能教育辅助系统
Corbett 和 Anderson将 BKT 模型应用于 ACT-R智能教育辅助系统中,用来判断学生知识水平,并且预测学生在相应学习行为之后的成绩表现。Pardos和 Heffeman在 2010 年提出个性化贝叶斯知识追踪模型中的初始学习参数p(),从而在智能辅助系统中更准确的评估学生的知识水平。在2011年,他们又将该模型应用于教育系统中,并有效扩展了项目难度,提高预测学生表现的准确性r。Baker和 Corbett”提出;使用机器学习来估计猜测和失误参数,简化贝叶斯知识追踪模型,并且这一方法更适合使用智能辅助系统中学生的表现数据。闾汉原,申麟“等通过将贝叶斯知识追踪模型嵌入到在线教育系统内,从而实现在学生完成作业后及时计算出其知识状态,起到查漏补缺的效果。
(2)在线视频课程
2013 年,Pardos等将贝叶斯知识追踪模型应用到 edx 慕课平台,通过对知识点划分、问题解答和测试等多种影响慕课平台的要素进行了调整,使该模型能够完全应用于视频课程。 Machardy等人通过使用 BKT 模型,开发了一个用水评价在线教育短视频使用情况的框架,并进一步探索了使用情况与测试结果的关系。王卓,张铭提出应用贝叶斯知识跟踪模型水对使用慕课学习的学生进行评价,根据 MOOC 的数据特点对模型进行调整,取得了较为理想的效果。2016年, Zhuo Wang, Zhiting Hu等人根据大型公开在线课程 Coursera, 通过使用BKT 模型,对知识状态的层次和时间属性进行建模,来对学生考试成绩进行预测。
(3)认知诊断
由于贝叶斯知识追踪模型可以用来评估学生知识水平和掌握情况,因此可以帮助教师更加准确的判断学生知识状态,从而提供更加针对性的教学帮助。Zhu Junhu, Zang Yichao”等人提出通过整合时间差异信息,结合贝叶斯知识追踪模型,根据学习者认知水平变化较大的拐点米获取知识状态,从而更好的避免认知诊断偏差。国内学者王军“通过将贝叶斯网络应用于学生认知诊断过程中,从而得到学习者的知识属性掌握水平。
整体而言,国内对于贝叶斯知识追踪模型的相关研究较少,将贝叶斯知识追踪模型应用到学生认知诊断中是一个较大的创新。这一方法可以更好的帮助教师了解到学生学习过程中不桥变化的知识状态,从而提供更加具有针对性的教学帮助,提升教学质量和学生学习效果。
-
7.3 深度知识点追踪模型(DKT)
7.3.1 DKT模型原理
DKT 模型主要采用循环神经网络(Recurrent Neural Network,RNN) ,对学习者的知识状态进行高维连续表征, 并利用其作答序列的时序关系信息进行题目作答对错的预测。
其基本原理是:将学生的答题记录 xt={qt, at}以独热编码或其它编码形式输入到 RNN 中,对学生的知识掌握状态进行建模,从而准确预测其未来的答题情况,并依据此为未来的智能化出题做参考,避免给学生出太难或太简单的题目。具体上,假设一个学生的答题记录为x0,x1,...,xt,我们要去预测下一个交互的情况xt+1,通常一次交互xt=(qt,at),qt代表该学生回答题目at的正误情况。简单的来说就是知道了学生答了一系列题目,也都知道他都回答对了没,现在我要从题库里再抽一题给他,让模型预测预测他能不能答对,答对的概率是多少,那么如果模型给出的概率是1,代表这题对他来说是太简单了,如果给出的概率为0,就代表这题可能太难了,他八成是做不出来的。
Deep Knowledge Tracing是用了RNN来把答题记录当做平常的时间序列来建模,至于RNN,下面简单列个公式表示一下。
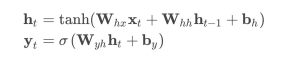
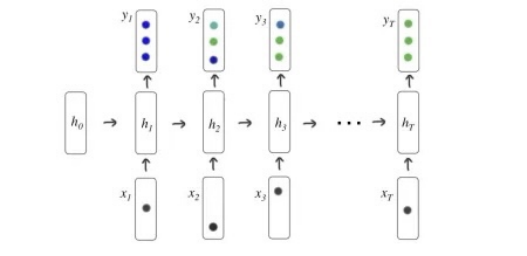
图7-3-1 基于RNN的DKT模型示意图
7.3.2 模型的输入和输出
假设数据集有M道题目,我们让xt为one-hot encoding,由于at∈RM,qt∈{0,1},那么xt∈R2M,即针对题目at有答对和答错两种不同的状态,所以one-hot的长度是2M。这时候很自然就能想到使用NLP中常用的Embedding,将每个one-hot向量通过embedding转为一个维度小得多的向量nat,qt∈RN,N<<M,这样每道题目就可以初始化为一个随机的低维向量表征,在之后的数据集上进行训练。
每个时间步,模型输入xt,输出yt∈RM,维度与题库大小相同,代表着学生答对每道题目的概率。我们根据yt可以选出下一题at+1的正确概率pt+1,再和真实的标签qt+1求交叉熵损失函数即: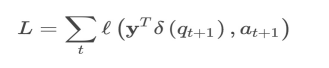
其中ℓ代表交叉熵损失函数,δ代表one-hot编码。
7.3.3 DKT模型实现
本文基于图注意力网络的可解释深度知识追踪框架,通过引入习题的上下文信息扩充习题知识点关系图,然后利用 RNN网络对答题序列建模得到用户当前的知识状态,最后基于用户知识状态学习注意力权重,得到当前预测习题基于用户知识状态的个性化表示,并为预测结果生成推理路径作为解释。模型由4个模块组成,分别为认知状态模块、基于用户知识状态的个性化习题表示模块、作答表现预测模块和解释路径生成模块。
(1) 认知状态模块
用于在用户交互序列中建模其知识状态,捕捉知识点间粗粒度的依赖关系。将序列最终时间步对应的隐藏状态作为当前用户状态表征,包含了用户对习题与对应知识点的掌握状态。
(2) 基于用户知识状态的个性化习题表示模块
本模块首先根据矩阵来构建知识点与习题之间关系的二部图,然后从所有用户交互信息中进一步建模知识点之间的联系、习题之间的共现关系等。这些上下文信息将用于扩展二部图,将知识点与习题之间的单一关系扩展为包含知识点间、习题间相关关系的图。然后对该图应用注意力图神经网络算法,由认知状态模块中获得的用户当前知识状态得到注意力值,据此聚合邻居节点信息,得到当前预测习题基于用户知识状态的表示。随后,该注意力加权的习题表示将与用户认知状态一道送入预测模块,预测用户作答表现。

图7-3-2 题-知识点关系图
(3) 作答表现预测模块
本模块根据之前得到的用户知识状态与个性化习题表示,输出用户在下一个时间步正确回答目标习题的概率。
(4) 解释路径生成模块
本模块在得到当前作答表现预测后,为预测结果提供可解释性。基于用户认知状态的个性化注意力可以使得用户关注的邻居节点得到更高的注意力值,因而对预测结果产生更大影响。由此,可利用该注意力值在图中为预测结果展示出一条推理路径。在每一跳邻居中选择最大注意值的节点添加到解释路径内,直至达到预定的跳数,就在习题知识点图中生成了一条解释路径,直观展示当前预测结果的产生原因。
如图7-3-3所示,根据个性化注意力权值,当前习题聚合跳内邻居的注意力权值分别为 0.5, 0.4, 0.1。因此我们将id为280的知识点和id为147382的习题分别加入推理序列中。重复以上过程,就可以在每一层邻居中选择注意力权值高的节点加入推理路径。由此,对于用户在当前习题的作答预测,IDKT生成了 2条推理路径:86623-280-310-309和 86623-147382-276。对照id的实际含义,就可以对所得推理路径进行解释。以推理路径1为例,模型预测用户未正确作答id为 86623的习题可能因为其考察了id为280的知识点。而知识点280与知识点310相关,由此得出的解释路径是,用户在知识点310存在薄弱环节导致当前习题没有回答正确。
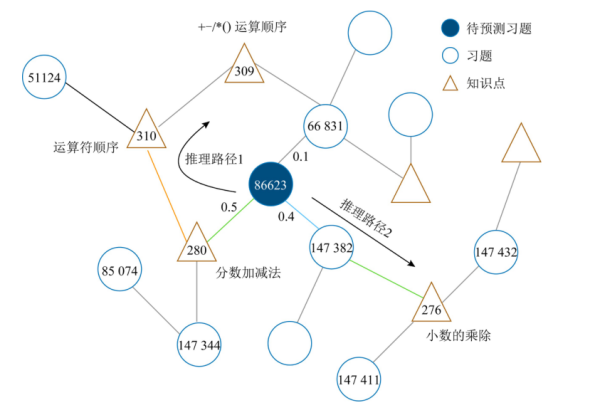
图7-3-3 可解释推理路径生成
7.3.3DKT模型的优缺点
优点
1、能根据学生最近的答题情况记录较长时间的知识情况。
2、能根据每次答题更新知识状态,只需要保存上一个隐层状态,不需要重复计算,适合线上部署。
3、不需要domain specific的知识,对任何用户答题数据集都适用。
4、能够自动捕捉相似题目之间的关联。
缺点
1、当答题序列被打乱时,模型输出的结果波动大,即相同的题目和相同的回答,当答题顺序不一致时,得到的知识状态不同。
2、由于上述问题,且学生在答题过程中对知识的掌握程度不一定具有连续一致性,导致对学生知识状态的预测受顺序影响发生偏差。
3、黑盒,有时会出现第一题答对导致对之后的预测概率都偏高,而第一题答错对之后的预测概率都偏低的奇怪情况。-
参考文献
【1】刘坤佳,李欣奕,唐九阳,赵翔.可解释深度知识追踪模型[J].计算机研究与发展,2021,58(12):2618-2629.
【2】卢宇,王德亮,章志,陈鹏鹤,余胜泉.智能导学系统中的知识追踪建模综述[J].现代教育技术,2021,31(11):87-95.
【3】李菲茗,叶艳伟,李晓菲,史丹丹.知识追踪模型在教育领域的应用:2008—2017年相关研究的综述[J].中国远程教育,2019(07):86-91.DOI:10.13541/j.cnki.chinade.20181214.001.
【4】张明心. 基于认知诊断的贝叶斯知识追踪模型改进与应用[D].华东师范大学,2019.
【5】曾凡智,许露倩,周燕,周月霞,廖俊玮.面向智慧教育的知识追踪模型研究综述[J].计算机科学与探索,2022,16(08):1742-1763.
【6】王卓,张铭.基于贝叶斯知识跟踪模型的慕课学生评价[J].中国科技论文,2015,10(02):241-246.
【7】陈之彧,单志龙.知识追踪研究进展[J].计算机科学,2022,49(10):83-95.
【8】王志锋,熊莎莎,左明章,闵秋莎,叶俊民.智慧教育视域下的知识追踪:现状、框架及趋势[J].远程教育杂志,2021,39(05):45-54.DOI:10.15881/j.cnki.cn33-1304/g4.2021.05.005.
【9】李蓬.深度知识追踪在适应性学习系统的应用[J].现代计算机,2021(16):27-31.
【10】张暖,江波.学习者知识追踪研究进展综述[J].计算机科学,2021,48(04):213-222.
【11】黄诗雯,刘朝晖,罗凌云,赵忠源,王璨.融合行为和遗忘因素的贝叶斯知识追踪模型研究[J].计算机应用研究,2021,38(07):1993-1997.DOI:10.19734/j.issn.1001-3695.2020.10.0356.
-
思考题
1.相较于BKT,DKT有何优势?
2.DKT是否存在不足?如果有,请简述。
3.针对BKT的种种不足,国内外学者进行了许多模型优化与扩展的研究,通过文献检索与分析,试例举一项通过对BKT优化发展而来的模型,并对其如何优化进行简述。
-
-
- 标签:
-
加入的知识群:


学习元评论 (0条)
聪明如你,不妨在这 发表你的看法与心得 ~