默认段落标题（请修改）...

社会网络分析方法是由社会学家根据数学方法﹑图论等发展起来的定量分析方法，近年来，该方法在职业流动、城市化对个体幸福的影响、世界政治和经济体系、国际贸易等领域广泛应用，并发挥了重要作用。社会网络分析是社会学领域比较成熟的分析方法，社会学家们利用它可以比较得心应手地来解释一些社会学问题。许多学科的专家如经济学、管理学等领域的学者们在新经济时代——知识经济时代，面临许多挑战时，开始考虑借鉴其他学科的研究方法，社会网络分析就是其中的一种。

　　网络指的是各种关联，而社会网络(Social Network)即可简单地称为社会关系所构成的结构。社会网络分析（Social Network Analysis，SNA）问题起源于物理学中的适应性网络，通过研究网络关系，有助于把个体间关系、“微观”网络与大规模的社会系统的“宏观”结构结合起来，通过数学方法﹑图论等定量分析方法，是20世纪70年代以来在社会学、心理学、人类学、数学、通信科学等领域逐步发展起来的一个的研究分支。

　　从社会网络的角度出发，人在社会环境中的相互作用可以表达为基于关系的一种模式或规则，而基于这种关系的有规律模式反映了社会结构，这种结构的量化分析是社会网络分析的出发点。社会网络分析不仅仅是一种工具，更是一种关系论的思维方式。可以利用来解释一些社会学、经济学、管理学等领域问题。近年来，该方法在职业流动、城市化对个体幸福的影响、世界政治和经济体系、国际贸易等领域广泛应用，并发挥了重要作用。

构成要素：

构成社会网络的主要要素有：

　　行动者(actor)：这里的行动者不但指具体的个人，还可指一个群体、公司或其他集体性的社会单位。每个行动者在网络中的位置被称为“结点(node)”。

　　关系纽带(relational tie)：行动者之间相互的关联即称关系纽带。人们之间的关系形式是多种多样的，如亲属关系、合作关系、交换关系、对抗关系等，这些都构成了不同的关系纽带。

　　二人组(dyad)：由两个行动者所构成的关系。这是社会网络的最简单或最基本的形式，是我们分析各种关系纽带的基础。

　　三人组(triad)：由三个行动者所构成的关系。

　　子群(subgroup)：指行动者之间的任何形式关系的子集。

　　群体(group)：其关系得到测量的所有行动者的集合。

社会网络分析法可以从多个不同角度对社会网络进行分析，包括中心性分析、凝聚子群分析、核心一边缘结构分析以及结构对等性分析等，这里仅介绍前3种。

分析角度：

　　中心性分析

　　“中心性”是社会网络分析的重点之一。个人或组织在其社会网络中具有怎样的权力，或者说居于怎样的中心地位，这一思想是社会网络分析者最早探讨的内容之一。个体的中心度(Centrality)测量个体处于网络中心的程度，反映了该点在网络中的重要性程度。因此一个网络中有多少个行动者／节点，就有多少个个体的中心度。除了计算网络中个体的中心度外，还可以计算整个网络的集中趋势(可简称为中心势)(Centralization)。与个体中心度刻画的是个体特性不同，网络中心势刻画的是整个网络中各个点的差异性程度，因此一个网络只有一个中心势。根据计算方法的不同，中心度和中心势都可以分为3种：点度中心度／点度中心势，中间中心度／中间中心势，接近中心度／接近中心势。

　　1.点度中心性在一个社会网络中，如果一个行动者与其他行动者之间存在直接联系，那么该行动者就居于中心地位，在该网络中拥有较大的“权力”。在这种思路的指导下，网络中一个点的点度中心度，就可以网络中与该点之间有联系的点的数目来衡量，这就是点度中心度。网络中心势指的是网络中点的集中趋势，它是根据以下思想进行计算的：首先找到图中的最大中心度数值；然后计算该值与任何其他点的中心度的差，从而得出多个“差值”；再计算这些“差值”的总和；最后用这个总和除以各个“差值”总和的最大可能值。

　　2.中间中心性在网络中，如果一个行动者处于许多其他两点之间的路径上，可以认为该行动者居于重要地位，因为他具有控制其他两个行动者之间的交往能力。根据这种思想来刻画行动者个体中心度的指标是中间中心度，它测量的是行动者对资源控制的程度。一个行动者在网络中占据这样的位置越多，就越代表它具有很高的中间中心性，就有越多的行动者需要通过它才能发生联系。中间中心势也是分析网络整体结构的一个指数，其含义是网络中中间中心性最高的节点的中间中心性与其他节点的中间中心性的差距。该节点与别的节点的差距越大，则网络的中间中心势越高，表示该网络中的节点可能分为多个小团体而且过于依赖某一个节点传递关系，该节点在网络中处于极其重要的地位。

　　3.接近中心性点度中心度刻画的是局部的中心指数，衡量的是网络中行动者与他人联系的多少，没有考虑到行动者能否控制他人。而中间中心度测量的是一个行动者“控制”他人行动的能力。有时还要研究网络中的行动者不受他人“控制”的能力，这种能力就用接近中心性来描述。在计算接近中心度的时候，我们关注的是捷径，而不是直接关系。如果一个点通过比较短的路径与许多其他点相连，我们就说该点具有较高的接近中心性。对一个社会网络来说，接近中心势越高，表明网络中节点的差异性越大，反之，则表明网络中节点间的差异越小。

　　凝聚子群分析

　　当网络中某些行动者之间的关系特别紧密，以至于结合成一个次级团体时，这样的团体在社会网络分析中被称为凝聚子群。分析网络中存在多少个这样的子群，子群内部成员之间关系的特点，子群之间关系特点，一个子群的成员与另一个子群成员之间的关系特点等就是凝聚子群分析。由于凝聚子群成员之间的关系十分紧密，因此有的学者也将凝聚子群分析形象地称为“小团体分析”。

　　1.凝聚子群根据理论思想和计算方法的不同，存在不同类型的凝聚子群定义及分析方法。

　　1)派系(Cliques)。在一个无向网络图中，“派系”指的是至少包含3个点的最大完备子图。这个概念包含3层含义：①一个派系至少包含三个点。②派系是完备的，根据完备图的定义，派系中任何两点之间都存在直接联系。③派系是“最大”的，即向这个子图中增加任何一点，将改变其“完备”的性质。

　　2)n-派系(n-Cliques)。对于一个总图来说，如果其中的一个子图满足如下条件，就称之为n-派系：在该子图中，任何两点之间在总图中的距离(即捷径的长度)最大不超过n。从形式化角度说，令d(i,j)代表两点和n在总图中的距离，那么一个n-派系的形式化定义就是一个满足如下条件的拥有点集的子图，即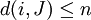：，对于所有的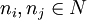，,来说，在总图中不存在与子图中的任何点的距离不超过n的点。

　　3)n-宗派(n—Clan)。所谓n-宗派(n—Clan)是指满足以下条件的n-派系，即其中任何两点之间的捷径的距离都不超过n。可见，所有的n-宗派都是n-派系。

　　4)k-丛(k-Plex)。一个k-丛就是满足下列条件的一个凝聚子群，即在这样一个子群中，每个点都至少与除了k个点之外的其他点直接相连。也就是说，当这个凝聚子群的规模为n时，其中每个点至少都与该凝聚子群中n-k个点有直接联系，即每个点的度数都至少为n—k。

　　2.凝聚子群密度凝聚子群的密度(External—Internal Index，E-I Index)主要用来衡量一个大的网络中小团体现象是否十分严重。这在分析组织管理等问题时十分有用。最糟糕的情形是大团体很散漫，核心小团体却有高度内聚力。另外一种情况就是大团体中有许多内聚力很高的小团体，很可能就会出现小团体间相互斗争的现象。凝聚子群密度的取值范围为[-1，+1]。该值越向1靠近，意味着派系林立的程度越大；该值越接近-1，意味着派系林立的程度越小；该值越接近0，表明关系越趋向于随机分布，看不出派系林立的情形。

　　E-I Index可以说是企业管理者的一个重要的危机指数。当一个企业的E-I Index过高时，就表示该企业中的小团体有可能结合紧密而开始图谋小团体私利，从而伤害到整个企业的利益。其实E-I Index不仅仅可以应用到企业管理领域，也可以应用到其他领域，比如用来研究某一学科领域学者之间的关系。如果该网络存在凝聚子群，并且凝聚子群的密度较高，说明处于这个凝聚子群内部的这部分学者之间联系紧密，在信息分享和科研合作方面交往频繁，而处于子群外部的成员则不能得到足够的信息和科研合作机会。从一定程度上来说，这种情况也是不利于该学科领域发展的。

　　核心一边缘结构分析

　　核心一边缘(Core—Periphery)结构分析的目的是研究社会网络中哪些节点处于核心地位，哪些节点处于边缘地位。核心边缘结构分析具有较广的应用性，可用于分析精英网络、科学引文关系网络以及组织关系网络等多种社会现象中的核心一边缘结构。

　　根据关系数据的类型(定类数据和定比数据)，核心—边缘结构有不同的形式。定类数据和定比数据是统计学中的基本概念，一般来说，定类数据是用类别来表示的，通常用数字表示这些类别，但是这些数值不能用来进行数学计算；而定比数据是用数值来表示的，可以用来进行数学计算。如果数据是定类数据，可以构建离散的核心一边缘模型；如果数据是定比数据，可以构建连续的核心一边缘模型。而离散的核心一边缘模型根据核心成员和边缘成员之间关系的有无及关系的紧密程度，又可分为3种：

　　①核心一边缘全关联模型；

　　②核心一边缘局部关联模型；

　　③核心一边缘关系缺失模型。

　　如果把核心和边缘之间的关系看成是缺失值，就构成了核心一边缘关系缺失模型。这里介绍适用于定类数据的4种离散的核心一边缘模型。

　　1)核心一边缘全关联模型。网络中的所有节点分为两组，其中一组的成员之间联系紧密，可以看成是一个凝聚子群(核心)，另外一组的成员之间没有联系，但是，该组成员与核心组的所有成员之间都存在关系。

　　2)核心一边缘无关模型。网络中的所有节点分为两组，其中一组的成员之间联系紧密，可以看成是一个凝聚子群(核心)，而另外一组成员之间则没有任何联系，并且同核心组成员之间也没有联系。

　　3)核心一边缘局部关联模型。网络中的所有节点分为两组，其中一组的成员之间联系紧密，可以看成是一个凝聚子群(核心)，而另外一组成员之间则没有任何联系，但是它们同核心组的部分成员之间存在联系。

　　4)核心一边缘关系缺失模型。网络中的所有节点分为两组，其中一组的成员之间的密度达到最大值，可以看成是一个凝聚子群(核心)，另外一组成员之间的密度达到最小值，但是并不考虑这两组成员之间关系密度，而是把它看作缺失值。

UCINET简介  

     UCINET为菜单驱动的Windows程序，可能是最知名和最经常被使用的处理社会网络数据和其他相似性数据的综合性分析程序。与UCINET捆绑在一 起的还有Pajek、Mage和NetDraw等三个软件。UCINET能够处理的原始数据为矩阵格式，提供了大量数据管理和转化工具。该程序本身不包含 网络可视化的图形程序，但可将数据和处理结果输出至NetDraw、Pajek、Mage和KrackPlot等软件作图。UCINET包含大量包括探测 凝聚子群（cliques, clans, plexes）和区域（components, cores）、中心性分析（centrality）、个人网络分析和结构洞分析在内的网络分析程序。UCINET还包含为数众多的基于过程的分析程序，如 聚类分析、多维标度、二模标度（奇异值分解、因子分析和对应分析）、角色和地位分析（结构、角色和正则对等性）和拟合中心-边缘模型。此外，UCINET 提供了从简单统计到拟合p1模型在内的多种统计程序。

Pajek简介

Pajek 是一个特别为处理大数据集而设计的网络分析和可视化程序。Pajek可以同时处理多个网络，也可以处理二模网络和时间事件网络（时间事件网络包括了某一网 络随时间的流逝而发生的网络的发展或进化）。Pajek提供了纵向网络分析的工具。数据文件中可以包含指示行动者在某一观察时刻的网络位置的时间标志，因 而可以生成一系列交叉网络，可以对这些网络进行分析并考察网络的演化。不过这些分析是非统计性的；如果要对网络演化进行统计分析，需要使用StOCNET 软件的SIENA模块。Pajek可以分析多于一百万个节点的超大型网络。Pajek提供了多种数据输入方式，例如，可以从网络文件（扩展名NET）中引 入ASCII格式的网络数据。网络文件中包含节点列表和弧/边（arcs/edges）列表，只需指定存在的联系即可，从而高效率地输入大型网络数据。图 形功能是Pajek的强项，可以方便地调整图形以及指定图形所代表的含义。由于大型网络难于在一个视图中显示，因此Pajek会区分不同的网络亚结构分别 予以可视化。每种数据类型在Pajek中都有自己的描述方法。Pajek提供的基于过程的分析方法包括探测结构平衡和聚集性 （clusterability），分层分解和团块模型（结构、正则对等性）等。Pajek只包含少数基本的统计程序。

NetMiner 简介

NetMiner 是一个把社会网络分析和可视化探索技术结合在一起的软件工具。它允许使用者以可视化和交互的方式探查网络数据，以找出网络潜在的模式和结构。 NetMiner采用了一种为把分析和可视化结合在一起而优化了的网络数据类型，包括三种类型的变量：邻接矩阵（称作层）、联系变量和行动者属性数据。与 Pajek和NetDraw相似，NetMiner也具有高级的图形特性，尤其是几乎所有的结果都是以文本和图形两种方式呈递的。NetMiner提供的 网络描述方法和基于过程的分析方法也较为丰富，统计方面则支持一些标准的统计过程：描述性统计、ANOVA、相关和回归。

STRUCTURE 简介

STRUCTURE 是一个命令驱动的DOS程序，需要在输入文件中包含数据管理和网络分析的命令。STRUCTURE支持五种网络分析类型中的网络模型：自主性（结构洞分 析）、凝聚性（识别派系）、扩散性、对等性（结构或角色对等性分析和团块模型分析）和权力（网络中心与均质分析）。STRUCTURE提供的大多数分析功 能是独具的，在其他分析软件中找不到。

MultiNet简介

 MultiNet 是一个适于分析大型和稀疏网络数据的程序。由于MultiNet是为大型网络的分析而专门设计的，因而像Pajek那样，数据输入也使用节点和联系列表， 而非邻接矩阵。对于分析程序产生的几乎所有输出结果都可以以图形化方式展现。MultiNet可以计算degree, betweenness, closeness and components statistic，以及这些统计量的频数分布。通过MultiNet，可以使用几种本征空间（eigenspace）的方法来分析网络的结构。 MultiNet包含四种统计技术：交叉表和卡方检验，ANOVA，相关和p*指数随机图模型。

StOCNET简介

StOCNET 是个WINDOWS环境下的开放软件系统，适用于社会网络的高级统计分析。它提供了一个应用多种统计方法的平台，每种统计方法可以以单独模块的形式方便地 嵌入其中。StOCNET包含六个统计模块：（1）BLOCKS，随机块模型；（2）ULTRAS，使用超度量（Ultrametrics）估计潜在的传 递性结构（latent transitive structures）；（3）P2，拟合指数随机图p2模型；（4）SIENA，纵向网络数据的分析；（5）ZO，确定随机图统计量的分布概率； （6）PACNET，构造和拟合基于偏代数结构的结构模型（structural models based on partial algebraic structures）。