识记：决策树模型和神经网络模型的概念。
理解：决策树学习策略和神经网络正反向传播及算法。
应用：能根据实际情况，灵活选择决策树或神经网络算法实现大学录取预测。

1.本章节重点是决策树模型和神经网络模型的概念及决策树和神经网路算法的应用。难点是通过决策树算法和神经网络算法实现大学录取预测。
2.课前，学生自行搭建部署算法实现环境，采用自主学习的方式浏览本章内容；课中，教师可以重点向学生呈现教学案例，组织学生开展主题研讨、案例分析、问题解决，让学生学会将算法应用于具体案例之中；课后，学生根据上课所学知识，寻找相关案例进行练习。
3.阅读相关的中英文文献有助于加深对本章的学习理解和应用
4.本课建议学时为6课时。

5.1.1 问题描述和定义

    随着教育信息化的发展，人工智能和智慧教育逐渐引领教育教学创新。教育大数据和教育人工智能的崛起使如何对大量数据进行分析以支持精准预测成为人工智能时代所面临的一个新课题。大学录取一直是国人较为关注的话题，对于各高校而言，如何高效便捷地对每年所报考的学生进行成绩的评估从而预测录取情况也成为重要的问题。决策树算法和神经网络算法作为机器学习领域的有效算法，已经广泛运用于教育教学，教育治理，教育评价的过程中，例如学生的学业成绩预测，学生画像等等。本章基于决策树算法和神经网络算法，将决策树算法和神经网络算法应用于美国某高校录取数据，采用Python语言建立模型，预测录取结果，并验证了模型的准确率。

5.1.2 数据描述和分析

        本实验选取了美国加州大学洛杉矶分校（UCLA）的研究生录取数据作为本实验的数据集。数据集中包含三类数据，分别是GRE、GPA和RANK。GRE表示学生研究生入学考试的成绩，GPA表示学生的绩点分数，RANK表示对于学生的评级。综合考虑以上三类数据而预测此学生是否能够被学校录取。我们使用data.describe( )：函数对于数据进行初步描述（如图所示）。

5.2.1 决策树模型

决策树( Decision Tree) 又称为判定树，是一种以树结构（包括二叉树和多叉树）形式来表达的预测分析模型。其每个非叶节点表示一个特征属性上的测试，每个分支代表这个特征属性在某个值域上的输出，而每个叶节点存放一个类别。

决策树中常用术语如下: 

(1)树枝→整棵树的划分称为树枝。

(2)根节点→代表进一步划分的整个样本。

(3)分裂→节点的划分称为分裂。

(4)终端节点→不进一步分裂的节点称为终端节点。

(5)决策节点→它是一个节点，它还被进一步划分为不同的子节点，即一个子节点。

(6)修剪→从决策节点中删除子节点。

(7)父节点和子节点→当一个节点被进一步划分时，该节点被称为父节点，而被划分的节点被称为子节点。

决策树模型的逻辑是，从根节点出发，对实例的每一个特征进行判断，根据判断结果，将实例分配到其子节点中，此时，每个节点又对应着该特征的一个取值，如此递归的对实例进行判断和分配，直至将实例分配到叶子结点中。

 

5.2.2 决策树学习策略

决策树学习过程可以分为3步，这3个步骤是:特征选择、决策树生成、决策树剪枝。不同的决策树算法，区别在于每个步骤上进行了不同的考虑和优化。

（1）特征选择

这一步主要根据特征选择算法来选取合适的特征来对当前样本集进行划分。在训练样本集中，每个样本的特征可能有很多个，不同特征对分类标签的作用有大有小。因而特征选择的作用就是筛选出跟分类标签最相关性的特征。在特征选择中通常使用的准则是:信息增益、信息增益率、基尼指数。

（2）决策树生成

选好特征后，就从当前树的根节点出发，根据该特征的不同取值建立子节点;对每个子节点使用相同的方式生成新的子节点，直到信息增益很小(满足一定的阈值)或者当前样本集不需要再划分为止。

（3）决策树剪枝

决策树剪枝的主要防止过拟合，通过提前去掉部分分支来降低过拟合的风险。剪枝的阈值设置是一个关键

 

5.2.3 决策树算法实现

（1）算法选择

在决策树模型构建过程中需依托相应的决策树算法，其主要包括ID3、C4.5、C5.0、CART 四种。

 

ID3算法

ID3算法在选择根节点和各内部节点中的分支属性时，采用信息增益作为评价标准。信息增益的缺点是倾向于选择取值较多的属性，在有些情况下这类属性可能不会提供太多有价值的信息.并且ID3算法只能对描述属性为离散型属性的数据集构造决策树。

 

C4.5算法

C4.5算法用信息增益率来选择属性，可以处理连续数值型属性，采用了一种后剪枝方法优点：产生的分类规则易于理解，准确率较高。缺点：在构造树的过程中，需要对数据集进行多次的顺序扫描和排序，因而导致算法的低效。此外，C4.5只适合于能够驻留于内存的数据集，当训练集大得无法在内存容纳时程序无法运行。

 

 C5.0算法

C5.0算法是在 ID3、C4.5算法基础上进行改进的，C5.0算法是一种多叉树算法，在决策树生长过程中采用的是最大信息增益率原则进行决策树节点和分裂点的选择，该算法只支持解决分类问题。

 

 CART算法

CART算法相比C5.0算法的分类方法，采用了简化的二叉树模型，其生长过程中采用的是最大基尼增益指数原则进行节点和分裂点的选择， CART 算法既可以解决分类问题也可以很好的处理预测问题。因此本研究选择CART决策树算法，作为构建决策树模型的主要算法。

 

（2）特征选择

在该数据集中“gpa”“gre”“rank”为预测列 X，“admit”为目标列y，并将数据集按8:2的比例分为训练集和测试集，其主要代码如下：

X=DataFrame(results,columns=[' gpa ',' gre ',' rank,'])

y=DataFrame(results,columns=['admit'])

X_train, X_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0)

 

（3）模型构建

本环节主要调用 python 算法包中的 DecisionTreeClassifier 库进行 CART决策树算法（gini 系数）课程成绩影响因素决策树模型的构建。

from sklearn import tree

model=tree.DecisionTreeClassifier(max_leaf_nades=16)

model=model.fit(X,y)

本文选择的是预剪枝的方法进行决策树的剪枝，在模型训练的过程中，事先决定决策树叶子的数量多次变动叶子数，对比最终模型的准确度和生成的PDF文档,最终决定叶子数为16时符合目的。

 

（4）模型可视化

根据决策树模型的训练，得出决策树模型，但是无法将决策树直观的呈现，本研究主要调用 pydotplus 包和 graphviz 图形可视化工具对决策树模型进行可视化处理，利用 pydotplus 包为 graphviz 语言提供 python 接口，从而实现 graphviz 对决策树模型可视化的一系列操作。

import graphviz

dot_data=tree.export_graphviz(model, out_file=None)

graph=graphviz.Source(dot_data)

graph.render("iris_decision_tree")

最终生成名为iris_decision_tree的PDF文件。

 

（5）模型准确率评估

利用测试集计算训练得出的模型准确率，代码如下：

model.score(X_test, y_test)

模型的准确率为0.6875。

 

      自从西班牙解剖学家Cajal于19世纪末创立了神经元学说以来，关于神经元的生物学特征和相关的电学性质在之后被相继发现^[1]。从此揭开了人类探索人脑奥秘的序幕，何为神经元呢？神经元又称神经细胞，是构成神经系统的基本单元。在人类的大脑皮层中大约有100亿个神经元，每个神经元通过刺激可以与成百上千的神经元建立连接并发送信号。神经元主要由细胞体、轴突和树突三个部分组成，具体如图5-3所示。

图5-3

       树突多呈树状分支，由细胞体向外伸出，树突可以接受刺激并将冲动传给细胞体。轴突是由细胞体向外伸出的一条粗细均匀、表面光滑的分支，用于传输神经冲动。末端常有分支,称为轴突终末，轴突末端常有分支，称为轴突末梢，将冲动从细胞体传向末梢。神经元之间通过轴突和树突相互连接，其接口称为突触。神经突触是调整神经元之间相互作用的基本结构功能单元。

       国际著名的神经网络专家、第一个计算机公司的创始人和神经网络实现技术的研究领导人 Hecht-Nielson给神经网络的定义是：“神经网络是一个以有向图为拓扑结构的动态系统，它通过对连续或断续式的输入作状态响应而进行信息处理”^[2]。

       神经网络系统是由大量的、同时也是很简单的处理单元（或称神经元），通过广泛地互相连接而形成的复杂网络系统。虽然每个神经元的结构和功能十分简单，但由大量神经元构成的网络系统的却颇为丰富与复杂。

神经网络系统是一个高度复杂的非线性动力学系统，不但具有一般非线性系统的共性，更主要的是它还具有自己的特点，比如高维性、神经元之间的广泛互连性以及自适应性或自组织性等。

 

5.3.1 神经网络正向传播

  在解释神经网络的前向传播时，将使用一个简单的全连接三层的神经网络进行说明，如下图5-3-1-1所示。

       

                                                                                             图5-3-1-1

  神经网络由一层一层的神经元构成（1纵列称为这个神经网络的一层），因此在学习神经网络的前向传播时，应该先知道每个神经元是如何计算的。

      单个神经元的计算

                 图中符号意义如下图5-3-2-2所示：

                  

                                                                                          图5-3-1-2
                ◆ 输入数据：x1，x2
                ◆ 权重参数：w1，w2
                ◆ 激活函数：f(e)
                ◆ 输出：y

  神经网络的正向传播算法，从输入层到隐藏层最后到输出层，依次计算每个神经元的状态值和激活值。

  用公式表示两层神经网络的前向传播过程：

                Layer 1:
                               Z^[1] = W^[1]·X + b^[1]
                               A^[1] = σ(Z^[1])
                Layer 2:
                               Z^[2] = W^[2]·A^[1] + b^[2]
                               A^[2] = σ(Z^[2])

  而我们知道，X其实就是A^[0]，所以不难看出:
  每一层的计算都是一样的：
               Layer i:
                            Z^[i] = W^[i]·A^[i-1] + b^[i]
                            A^[i] = σ(Z^[i])

  因此，其实不管我们神经网络有几层，都是将上面过程的重复。

  对于损失函数，就跟Logistic regression中的一样，使用“交叉熵（cross-entropy）”，公式就是

• 二分类问题：
  L(y^,y) = -[y·log(y^ )+(1-y)·log(1-y^ )] 
• 多分类问题：
  L=-Σy_(j)·y^_(j) 

  这个是每个样本的loss，我们一般还要计算整个样本集的loss，也称为cost，用J表示，J就是L的平均：
            J(W,b) = 1/m·ΣL(y^⁽ⁱ⁾,y⁽ⁱ⁾)

  上面的求Z、A、L、J的过程就是正向传播。

 

5.3.2 神经网络反向传播     

  反向传播算法(Backpropagation，简称BP算法)是“误差反向传播”的简称，是适合于多层神经元网络的一种学习算法，它建立在梯度下降法的基础上。梯度下降法是训练神经网络的常用方法，许多的训练方法都是基于梯度下降法改良出来的，因此了解梯度下降法很重要。梯度下降法通过计算损失函数的梯度，并将这个梯度反馈给最优化函数来更新权重以最小化损失函数。

BP算法的学习过程由正向传播过程和反向传播过程组成。

　在正向传播过程中，输入信息通过输入层经隐含层，逐层处理并传向输出层。如果预测值和教师值不一样，则取输出与期望的误差的平方和作为损失函数（损失函数有很多，这是其中一种）。将正向传播中的损失函数传入反向传播过程，逐层求出损失函数对各神经元权重的偏导数，作为目标函数对权重的梯度。根据这个计算出来的梯度来修改权重，网络的学习在权重修改过程中完成。误差达到期望值时，网络学习结束。

 BP算法主要用在神经网络（深度学习）中，大多数情况下，神经网络求损失函数对中间层参数的导数是一件十分困难的事情，但BP算法能很好的解决这个问题。BP算法最重要的两个步骤分别是Forward pass和Backward pass。首先我们知道BP算法的目的是求损失函数对权重/偏置参数的导数，即求：

     ∂L(θ)∂w=∑n=1N∂Cn(θ)∂w

     即，求∂C(θ)∂w,∂L(θ)∂b 即可。C(θ)是代价函数，它是y和y^的距离度量，将所有的训练集的代价函数求和即为损失函数

  我们以对一个神经元求 ∂C∂w 为例，根据链式求导法则：

     ∂C∂w=∂z∂w∂C∂z

     z=∑imxiwi+b

     z作为此神经元的最终输入，m为此神经元的初始输入（也是前一层神经元的输出）x的个数，b为偏置。

  所以我们目标即转化成了求∂z∂w，∂C∂z。实际上Forward pass就是用来计算∂z∂的，而Backward pass是用来求∂C∂z的。

  Forward pass

     Forward pass非常简单,因为根据求导公式：

     ∂z∂wi=xi

  所以∂z∂w的值就是这个权重关联的输入x（实际上x也是中间层hidden layer的输出，后面我们把这个输出用a表示，实际上是一个东西）

  我们给一个直观的前向传播图，如图5-3-2-1所示：

                 

                                                                                                                                 图5-3-2-1

  Backward pass

  在神经网络模型定义好后，神经元的激活函数σ(z)（activation function）已经确定,我们定义a为一个神经元的输出，那么我们根据链式求导法则：

      ∂C∂z=∂a∂z∂C∂a

      由于a=σ(z)，所以∂a∂z=σ′(z)=const

      所以目标转化为求∂C∂a

  我们知道：

      z=∑aw

      由链式法则可得：

      ∂C∂a=∂z(1)∂a∂C∂z(1)+∂z(2)∂a∂C∂z(2)+...+∂z(k)∂a∂C∂z(k)=∑i=1k∂z(i)∂a∂C∂z(i)

      k为此神经元输出到后层神经元的个数，即与此神经元输出相关的权重个数

  所以 ∂z∂a=w

  为便于理解，我们以下图5-3-2-2为例：

             

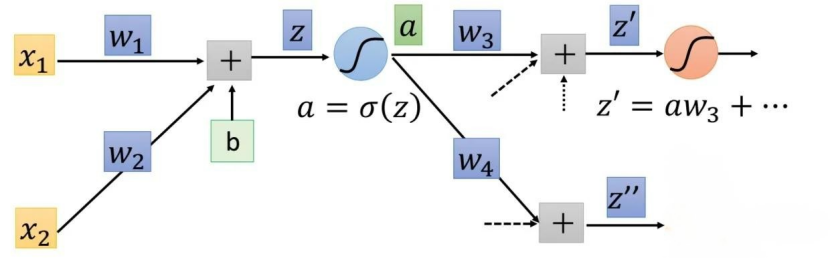
                                                                                                                                图5-3-2-2

 

  根据上图

     ∂C∂z=σ′(z)(w3∂C∂z′+w4∂C∂z′′)

  实际上我们就是利用上式进行反向迭代（Backward pass），之所以叫Backward pass是因为我们是从最后一层开始计算的，即从输出层开始计算。在这里我们给一个简单的网络，如图5-3-2-3所示：

                                            

                                                                                                                             图5-3-2-3
  该输出层的计算如下：

     ∂C∂z′=∂y1∂z′∂C∂y1,∂C∂z′′=∂y2∂z′′∂C∂y2

  当我们从输出层开始计算时，由于∂C∂yi是可以直接求得的，所以最后一层的∂C∂z是可以求得的。所以Backward pass的原理图如图5-3-3-4所示：

                                                         

                                                                                                                                       图5-3-2-4
   根据上图：∂C(n−2)∂z(n−2)=σ′(z(n−2))∑w∂C(n)∂z(n)

   所以Backward pass就是先求出最后一层的∂C∂z，再通过上式一步步反向进行求出每一层的偏导∂C∂z。

   计算结果

   由于Forward Pass已经计算出∂z∂w=a，Backward pass已经求出∂C∂z，我们只要令其对应相乘即可得∂C∂w。

 

5.3.3 神经网络算法实现

我们基于以下三条数据对加州大学洛杉矶分校 (UCLA) 的研究生录取情况进行预测：

• GRE 分数（测试）即 GRE Scores (Test)
• GPA 分数（成绩）即 GPA Scores (Grades)
• 评级（1-4）即 Class rank (1-4)

1.加载数据

导入 pandas 和 numpy 两个数据包

# Importing pandas and numpy

import pandas as pd

import numpy as np

 

# Reading the csv file into a pandas DataFrame

data = pd.read_csv('student_data.csv')

 

# Printing out the first 10 rows of our data

data[:10]

 

2.绘制图形

首先让我们对数据进行绘图，看看它是什么样的。为了绘制二维图，让我们先忽略评级 (rank)。

# Importing matplotlib

import matplotlib.pyplot as plt

%matplotlib inline

# Function to help us plot

def plot_points(data):

    X = np.array(data[["gre","gpa"]])

    y = np.array(data["admit"])

    admitted = X[np.argwhere(y==1)]

    rejected = X[np.argwhere(y==0)]

    plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'red', edgecolor = 'k')

    plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'cyan', edgecolor = 'k')

    plt.xlabel('Test (GRE)')

    plt.ylabel('Grades (GPA)')

    

# Plotting the points

plot_points(data)

plt.show()

 

粗略来说，它看起来像是，成绩 （grades) 和测试 (test) 分数高的学生通过了，而得分低的学生却没有，但数据并没有如我们所希望的那样，很好地分离。 也许将评级 (rank) 考虑进来会有帮助？ 接下来我们将绘制 4 个图，每个图代表一个级别。

# Separating the ranks

data_rank1 = data[data["rank"]==1]

data_rank2 = data[data["rank"]==2]

data_rank3 = data[data["rank"]==3]

data_rank4 = data[data["rank"]==4]

​

# Plotting the graphs

plot_points(data_rank1)

plt.title("Rank 1")

plt.show()

plot_points(data_rank2)

plt.title("Rank 2")

plt.show()

plot_points(data_rank3)

plt.title("Rank 3")

plt.show()

plot_points(data_rank4)

plt.title("Rank 4")

plt.show()

 

 

 

现在看起来更棒啦，看上去评级越低，录取率越高。 让我们使用评级 (rank) 作为我们的输入之一。 为了做到这一点，我们应该对它进行一次one-hot 编码。

3.将评级进行 One-hot 编码

我们将在 Pandas 中使用 get_dummies 函数。

# TODO:  Make dummy variables for rank

one_hot_data = None

 

# TODO: Drop the previous rank column

one_hot_data = None

 

# Print the first 10 rows of our data

one_hot_data[:10]

 

4.进行缩放数据

下一步是缩放数据。 我们注意到成绩 (grades) 的范围是 1.0-4.0，而测试分数 （test scores) 的范围大概是 200-800，这个范围要大得多。 这意味着我们的数据存在偏差，使得神经网络很难处理。 让我们将两个特征放在 0-1 的范围内，将分数除以 4.0，将测试分数除以 800。

# Making a copy of our data

processed_data = one_hot_data[:]

 

# TODO: Scale the columns

processed_data['gre'] = processed_data['gre']/800

processed_data['gpa'] = processed_data['gpa']/800

# Printing the first 10 rows of our procesed data

processed_data[:10]

 

5.将数据分成训练集和测试集

为了测试我们的算法，我们将数据分为训练集和测试集。 测试集的大小将占总数据的 10％。

sample = np.random.choice(processed_data.index,size=int(len(processed_data)*0.9), replace=False)

 

train_data, test_data = processed_data.iloc[sample], processed_data.drop(sample)

 

print("Number of training samples is", len(train_data))

print("Number of testing samples is", len(test_data))

print(train_data[:10])

print(test_data[:10])

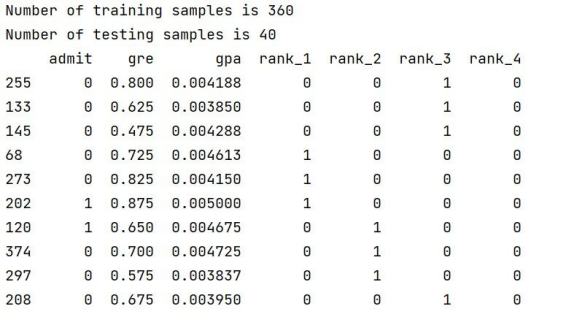
6.将数据分成特征和目标（标签）

现在，在培训前的最后一步，我们将把数据分为特征 (features)（X）和目标 (targets)（y）。

features = train_data.drop('admit', axis=1)

targets = train_data['admit']

features_test = test_data.drop('admit', axis=1)

targets_test = test_data['admit']

​

print(features[:10])

print(targets[:10])

 

7.训练二层神经网络

下列函数会训练二层神经网络。 首先，我们将写一些 helper 函数。

# Activation (sigmoid) function

def sigmoid(x):

    return 1 / (1 + np.exp(-x))

def sigmoid_prime(x):

    return sigmoid(x) * (1-sigmoid(x))

def error_formula(y, output):

    return - y*np.log(output) - (1 - y) * np.log(1-output)

 

8.误差反向传播

 

# TODO: Write the error term formula

def error_term_formula(y, output):

    pass

# Neural Network hyperparameters

epochs = 1000

learnrate = 0.5

​

# Training function

def train_nn(features, targets, epochs, learnrate):

    

    # Use to same seed to make debugging easier

    np.random.seed(42)

​

    n_records, n_features = features.shape

    last_loss = None

​

    # Initialize weights

    weights = np.random.normal(scale=1 / n_features**.5, size=n_features)

​

    for e in range(epochs):

        del_w = np.zeros(weights.shape)

        for x, y in zip(features.values, targets):

            # Loop through all records, x is the input, y is the target

​

            # Activation of the output unit

            #   Notice we multiply the inputs and the weights here

            #   rather than storing h as a separate variable

            output = sigmoid(np.dot(x, weights))

​

            # The error, the target minus the network output

            error = error_formula(y, output)

​

            # The error term

            #   Notice we calulate f'(h) here instead of defining a separate

            #   sigmoid_prime function. This just makes it faster because we

            #   can re-use the result of the sigmoid function stored in

            #   the output variable

            error_term = error_term_formula(y, output)

​

            # The gradient descent step, the error times the gradient times the inputs

            del_w += error_term * x

​

        # Update the weights here. The learning rate times the

        # change in weights, divided by the number of records to average

        weights += learnrate * del_w / n_records

​

        # Printing out the error on the training set

        if e % (epochs / 10) == 0:

            out = sigmoid(np.dot(features, weights))

            loss = np.mean((out - targets) ** 2)

            print("Epoch:", e)

            if last_loss and last_loss < loss:

                print("Train loss: ", loss, "  WARNING - Loss Increasing")

            else:

                print("Train loss: ", loss)

            last_loss = loss

            print("=========")

    print("Finished training!")

    return weights

    

weights = train_nn(features, targets, epochs, learnrate)

 

9.计算测试 (Test) 数据的精确度

# Calculate accuracy on test data

tes_out = sigmoid(np.dot(features_test, weights))

predictions = tes_out > 0.5

accuracy = np.mean(predictions == targets_test)

print("Prediction accuracy: {:.3f}".format(accuracy))

1.请简要概述逻辑树模型和神经网络模型。

2.请说一说决策树模型的优缺点。

3.请写出神经网络正向传播和反向传播的不同。

4.请动手利用神经网络算法实现加州洛杉矶大学研究生的录取。

[1]焦李成,杨淑媛,刘芳,王士刚,冯志玺.神经网络七十年:回顾与展望[J].计算机学报,2016,39(08):1697-1716.

[2]Arel I, Rose D C, Karnowski T P. Deep machine learning-a new frontier in artificial intelligence research [research frontier][J]. IEEE computational intelligence magazine, 2010, 5(4): 13-18.

[3]Werbos P J. Computational intelligence for the smart grid-history, challenges, and opportunities[J]. IEEE Computational Intelligence Magazine, 2011, 6(3): 14-21.Bengio Y. Learning deep architectures for AI[J]. Foundations and trends® in Machine Learning, 2009, 2(1): 1-127.

[4]刘志妩. 基于决策树算法的学生成绩的预测分析[J]. 计算机应用与软件, 2012, 29(11):4.

[5]武彤, 王秀坤. 决策树算法在学生成绩预测分析中的应用[J]. 微计算机信息, 2010(3):3.

[6]邵旻晖. 决策树典型算法研究综述[J]. 2018.